
°æƒø°øƒ≥µÿ«¯2007ƒÍ÷¡2013ƒÍ≈©¥Âæ”√Òº“Õ•¥ø ’»Îy£®µ•Œª£∫«ß‘™£©µƒ ˝æð»Áœ¬±Ì£∫
ƒÍ∑ð | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
ƒÍ∑ð¥˙∫≈t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
»Àæ˘¥ø ’»Îy | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
£®1£©«Ûyπÿ”⁄tµƒœþ–‘ªÿπÈ∑Ω≥ãª
£®2£©¿˚”√£®1£©÷–µƒªÿπÈ∑Ω≥ã¨∑÷Œˆ2007ƒÍ÷¡2013ƒÍ∏√µÿ«¯≈©¥Âæ”√Òº“Õ•»Àæ˘¥ø ’»Îµƒ±‰ªØ«Èøˆ£¨≤¢‘§≤‚∏√µÿ«¯2015ƒÍ≈©¥Âæ”√Òº“Õ•»Àæ˘¥ø ’»Î.
∏Ω£∫ªÿπÈ÷±œþµƒ–±¬ ∫ÕΩÿæýµƒ◊Ó–°∂˛≥À∑®π¿º∆π´ Ω∑÷±Œ™£∫
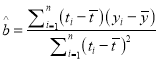 £¨
£¨ ![]()
°æ¥∞∏°ø£®1£©![]() £ª£®2£©6.8«ß‘™.
£ª£®2£©6.8«ß‘™.
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©∏˘æðÀ˘∏¯µƒ ˝æ𣨿˚”√◊Ó–°∂˛≥À∑®ø…µ√∫·±Í∫Õ◊ð±Íµƒ∆Ωæ˘ ˝£¨∫·±Í∫Õ◊ð±Íµƒª˝µƒ∫Õ£¨”Î∫·±Íµƒ∆Ω∑Ω∫Õ£¨¥˙»Îπ´ Ω«Û≥ˆbµƒ÷µ£¨‘Ÿ«Û≥ˆaµƒ÷µ£¨–¥≥ˆœþ–‘ªÿπÈ∑Ω≥ãÆ
£®2£©∏˘æð…œ“ªŒ ◊ˆ≥ˆµƒœþ–‘ªÿπÈ∑Ω≥㨥˙»ÎÀ˘∏¯µƒtµƒ÷µ£¨‘§≤‚∏√µÿ«¯2015ƒÍ≈©¥Âæ”√Òº“Õ•»Àæ˘¥ø ’»Î£¨’‚ «“ª∏ˆπ¿º∆÷µ.
‘Ã‚Ω‚Œˆ£∫£®1£©”…“‚£¨ ![]() ,
,
![]() ,
,
![]() ,
,
![]()
°ýyπÿ”⁄tµƒœþ–‘ªÿπÈ∑Ω≥ÃŒ™![]() £ª 8∑÷
£ª 8∑÷
£®2£©”…£®1£©÷™£¨b=0.5£æ0£¨π 2007ƒÍ÷¡2013ƒÍ∏√µÿ«¯≈©¥Âæ”√Òº“Õ•»Àæ˘¥ø ’»Î÷ƒÍ‘ˆº”£¨∆Ωæ˘√øƒÍ‘ˆº”0.5«ß‘™£Æ
Ω´2015ƒÍµƒƒÍ∑ð¥˙∫≈t=9¥˙»Î![]() ,µ√£∫
,µ√£∫ ![]() («ß‘™)
(«ß‘™)
𠑧≤‚∏√µÿ«¯2015ƒÍ≈©¥Âæ”√Òº“Õ•»Àæ˘¥ø ’»ÎŒ™6.8«ß‘™◊Û”“. 12∑÷



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™ ˝¡–{an}£¨¬˙◊„a1=1£¨ ![]() £¨n° N* £Æ £®¢Ò£©«Û÷§£∫ ˝¡–
£¨n° N* £Æ £®¢Ò£©«Û÷§£∫ ˝¡– ![]() Œ™µ»≤Ó ˝¡–£ª
Œ™µ»≤Ó ˝¡–£ª
£®¢Ú£©…Ë ![]() £¨«ÛT2n £Æ
£¨«ÛT2n £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £Æ
£Æ
£®1£©«Û![]() ‘⁄
‘⁄![]() …œµƒ◊Ó–°÷µ£ª
…œµƒ◊Ó–°÷µ£ª
£®2£©»Ùπÿ”⁄![]() µƒ≤ªµ» Ω
µƒ≤ªµ» Ω![]() ÷ª”–¡Ω∏ˆ’˚ ˝Ω‚£¨«Û µ ˝
÷ª”–¡Ω∏ˆ’˚ ˝Ω‚£¨«Û µ ˝![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ´±ý∫≈Œ™1°¢2°¢3°¢4µƒÀƒ∏ˆ–°«ÚÀʪ˙µƒ∑≈»Î±ý∫≈Œ™1°¢2°¢3°¢4µƒÀƒ∏ˆ÷Ωœ‰÷–£¨√ø∏ˆ÷Ωœ‰”–«“÷ª”–“ª∏ˆ–°«Ú£¨≥∆¥ÀŒ™“ª¬÷°∞∑≈«Ú°±£Æ…Ë“ª¬÷°∞∑≈«Ú°±∫Û±ý∫≈Œ™![]() µƒ÷Ωœ‰∑≈»Îµƒ–°«Ú±ý∫≈Œ™
µƒ÷Ωœ‰∑≈»Îµƒ–°«Ú±ý∫≈Œ™![]() £¨∂®“ÂŒ«∫œ∂»ŒÛ≤ÓŒ™
£¨∂®“ÂŒ«∫œ∂»ŒÛ≤ÓŒ™![]()
![]()
(1) –¥≥ˆŒ«∫œ∂»ŒÛ≤Ó![]() µƒø…ƒÐ÷µºØ∫œ£ª
µƒø…ƒÐ÷µºØ∫œ£ª
(2) ºŸ…Ë![]() µ»ø…ƒÐµÿŒ™1£¨2£¨3£¨4µƒ∏˜÷÷≈≈¡–£¨«ÛŒ«∫œ∂»ŒÛ≤Ó
µ»ø…ƒÐµÿŒ™1£¨2£¨3£¨4µƒ∏˜÷÷≈≈¡–£¨«ÛŒ«∫œ∂»ŒÛ≤Ó![]() µƒ∑÷≤º¡–£ª
µƒ∑÷≤º¡–£ª
(3)ƒ≥»À¡¨–¯Ω¯––¡ÀÀƒ¬÷°∞∑≈«Ú°±£¨»Ù∂º¬˙◊„![]() £¨ ‘∞¥(¢Ú)÷–µƒΩ·π˚£¨º∆À„≥ˆœ÷’‚÷÷œ÷œÛµƒ∏≈¬ (ºŸ∂®∏˜¬÷°∞∑≈«Ú°±œýª•∂¿¡¢)£ª
£¨ ‘∞¥(¢Ú)÷–µƒΩ·π˚£¨º∆À„≥ˆœ÷’‚÷÷œ÷œÛµƒ∏≈¬ (ºŸ∂®∏˜¬÷°∞∑≈«Ú°±œýª•∂¿¡¢)£ª
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥∆Û“µ…˙≤˙º◊°¢““¡Ω÷÷≤˙∆∑£¨“—÷™…˙≤˙√ø∂÷º◊≤˙∆∑“™”√A‘≠¡œ3∂÷£¨B‘≠¡œ2∂÷£¨…˙≤˙√ø∂÷““≤˙∆∑“™”√A‘≠¡œ1∂÷£¨B‘≠¡œ3∂÷°£œ˙ €√ø∂÷º◊≤˙∆∑ø…ªÒµ√¿˚»Û5ÕÚ‘™£¨√ø∂÷““≤˙∆∑ø…ªÒµ√¿˚»Û3ÕÚ‘™£¨∏√∆Û“µ‘⁄“ª∏ˆ…˙≤˙÷Ð∆⁄ƒ⁄œ˚∫ƒA‘≠¡œ≤ª≥¨π˝13∂÷£¨B‘≠¡œ≤ª≥¨π˝18∂÷£¨ƒ«√¥∏√∆Û“µø…ªÒµ√◊Ó¥Û¿˚»Û «___________ÕÚ‘™
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øπ˝µ„A£®4£¨1£©µƒ‘≤C”Î÷±œþx©Åy©Å1=0œý«–”⁄µ„B£®2£¨1£©£¨‘Ú‘≤Cµƒ∑Ω≥ÃŒ™ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
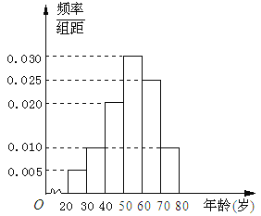
°æƒø°ø°∞÷–π˙»Àæ˘∂¡ È4.3±æ£®∞¸¿®Õ¯¬ÁŒƒ—ß∫ÕΩÃø∆ È£©£¨±»∫´π˙µƒ11±æ°¢∑®π˙µƒ20±æ°¢»’±æµƒ40±æ°¢”Ãô»Àµƒ64±æ…Ÿµ√∂ý£¨ « ¿ΩÁ…œ»Àæ˘∂¡ È◊Ó…Ÿµƒπ˙º“.°±’‚∏ˆ¬€∂œ±ª∏˜÷÷√ΩÃÂ∑¥∏¥“˝”√.≥ˆœ÷’‚—˘µƒÕ≥º∆Ω·π˚ŒÞ“… «¡Ó»Àޜތµƒ£¨∂¯«“∫Õ∆‰À˚π˙º“œý±»£¨Œ“π˙π˙√Òµƒ‘ƒ∂¡¡ø»Á¥À÷Ƶգ¨“≤∫ÕŒ“π˙ «¥´Õ≥µƒŒƒ√˜π≈π˙°¢¿Ò“«÷Æ∞ÓµƒµÿŒª≤ªœý∑˚.ƒ≥–°«¯Œ™¡À÷∏þ–°«¯ƒ⁄»À‘±µƒ∂¡ È–À»§£¨ÃÿæŸ∞Ï∂¡ ȪÓ∂Ø£¨◊º±∏Ω¯“ª∂®¡øµƒ ȺÆ∑·∏ª–°«¯Õº Ȓ棨”…”⁄≤ªÕ¨ƒÍ¡‰∂Œ–Ëø¥≤ªÕ¨¿ý–Õµƒ Ⱥƣ¨Œ™¡À∫œ¿Ì≈‰±∏◊ ‘¥£¨œ÷∂‘–°«¯ƒ⁄ø¥ È»À‘±Ω¯––ƒÍ¡‰µ˜≤È£¨Àʪ˙≥È»°¡À“ªÃÏ![]() √˚∂¡ È’þΩ¯––µ˜≤È£¨Ω´À˚√«µƒƒÍ¡‰∑÷≥…6∂Œ£∫
√˚∂¡ È’þΩ¯––µ˜≤È£¨Ω´À˚√«µƒƒÍ¡‰∑÷≥…6∂Œ£∫![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() ∫Ûµ√µΩ»ÁÕºÀ˘ 浃∆µ¬ ∑÷≤º÷±∑ΩÕº£ÆŒ £∫
∫Ûµ√µΩ»ÁÕºÀ˘ 浃∆µ¬ ∑÷≤º÷±∑ΩÕº£ÆŒ £∫
£®1£©π¿º∆‘⁄40√˚∂¡ È’þ÷–ƒÍ¡‰∑÷≤º‘⁄![]() µƒ»À ˝£ª
µƒ»À ˝£ª
£®2£©«Û40√˚∂¡ È’þƒÍ¡‰µƒ∆Ωæ˘ ˝∫Õ÷–Œª ˝£ª
£®3£©»Ù¥”ƒÍ¡‰‘⁄![]() µƒ∂¡ È’þ÷–»Œ»°2√˚£¨«Û’‚¡Ω√˚∂¡ È’þƒÍ¡‰‘⁄
µƒ∂¡ È’þ÷–»Œ»°2√˚£¨«Û’‚¡Ω√˚∂¡ È’þƒÍ¡‰‘⁄![]() µƒ»À ˝
µƒ»À ˝![]() µƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚£Æ
µƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÀÊ◊≈ ÷ª˙ π”√µƒ≤ª∂œ∆’º∞£¨œ÷‘⁄»´π˙∏˜µÿµƒ÷––°—ß…˙–Ø¥¯ ÷ª˙Ω¯»Î–£‘∞“—æ≠≥…Œ™¡À∆’±Èµƒœ÷œÛ£¨“≤“˝∆¡À“ªœµ¡–µƒŒ °£»ª∂¯£¨ «∂¬ªπ « Ë£¨æÕ∞⁄‘⁄¡ÀŒ“√«—ß–£¿œ ¶µƒ√Ê«∞£Æƒ≥—–æø–Õ—ßœ∞–°◊ȵ˜≤È—–æø°∞÷–—ß…˙ π”√ ÷ª˙∂‘—ßœ∞µƒ”∞œÏ°±£¨≤ø∑÷Õ≥º∆ ˝æð»Áœ¬±Ì£∫
≤ª π”√ ÷ª˙ | π”√ ÷ª˙ | ∫œº∆ | |
—ßœ∞≥…º®”≈–„»À ˝ | 18 | 7 | 25 |
—ßœ∞≥…º®≤ª”≈–„»À ˝ | 6 | 19 | 25 |
∫œº∆ | 24 | 26 | 50 |
≤Œøº ˝æð£∫![]() £¨∆‰÷–
£¨∆‰÷–![]() £Æ
£Æ
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
£®1£© ‘∏˘æð“‘…œ ˝æ𣨑À”√∂¿¡¢–‘ºÏ—ÈÀºœÎ£¨÷∏≥ˆ”–∂ý¥Û∞—Œ’»œŒ™÷–—ß…˙ π”√ ÷ª˙∂‘—ßœ∞”–”∞œÏ?
£®2£©—–æø–°◊ÈΩ´∏√—˘±æ÷– π”√ ÷ª˙«“≥…º®”≈–„µƒ7ŒªÕ¨—ߺ«Œ™![]() ◊È£¨≤ª π”√ ÷ª˙«“≥…º®”≈–„µƒ18ŒªÕ¨—ߺ«Œ™
◊È£¨≤ª π”√ ÷ª˙«“≥…º®”≈–„µƒ18ŒªÕ¨—ߺ«Œ™![]() ◊È£¨º∆ªÆ¥”
◊È£¨º∆ªÆ¥”![]() ◊ÈÕ∆—°µƒ2»À∫Õ
◊ÈÕ∆—°µƒ2»À∫Õ![]() ◊ÈÕ∆—°µƒ3»À÷–£¨Àʪ˙ÃÙ—°¡Ω»À¿¥∑÷œÌ—ßœ∞æ≠—ȣƫÛÃÙ—°µƒ¡Ω»À÷–“ª»À¿¥◊‘
◊ÈÕ∆—°µƒ3»À÷–£¨Àʪ˙ÃÙ—°¡Ω»À¿¥∑÷œÌ—ßœ∞æ≠—ȣƫÛÃÙ—°µƒ¡Ω»À÷–“ª»À¿¥◊‘![]() ◊È°¢¡Ì“ª»À¿¥◊‘
◊È°¢¡Ì“ª»À¿¥◊‘![]() ◊ȵƒ∏≈¬ £Æ
◊ȵƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…ËAB=6£¨‘⁄œþ∂ŒAB…œ»Œ»°¡Ωµ„C°¢D£®∂Àµ„A°¢B≥˝Õ‚£©£¨Ω´œþ∂ŒAB∑÷≥…»˝Ãıœþ∂ŒAC°¢CD°¢DB£Æ
£®1£©»Ù∑÷≥…µƒ»˝Ãıœþ∂Œµƒ≥§∂»æ˘Œ™’˝’˚ ˝£¨«Û’‚»˝Ãıœþ∂Œø…“‘ππ≥…»˝Ω«–Œ£®≥∆Œ™ ¬º˛A£©µƒ∏≈¬ £ª
£®2£©»Ù∑÷≥…µƒ»˝Ãıœþ∂Œµƒ≥§∂»æ˘Œ™’˝ µ ˝£¨«Û’‚»˝Ãıœþ∂Œø…“‘ππ≥…»˝Ω«–Œ£®≥∆Œ™ ¬º˛B£©µƒ∏≈¬ £ª
£®3£©∏˘æð“‘œ¬”√º∆À„ª˙À˘≤˙…˙µƒ20◊ÈÀʪ˙ ˝£¨ ‘”√Àʪ˙ ˝ƒ£ƒ‚µƒ∑Ω∑®£¨¿¥Ω¸À∆º∆À„£®2£©÷– ¬º˛Bµƒ∏≈¬ £¨ 20◊ÈÀʪ˙ ˝»Áœ¬£∫
◊ȱ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
X | 0.52 | 0.36 | 0.58 | 0.73 | 0.41 | 0.6 | 0.05 | 0.32 | 0.38 | 0.73 |
Y | 0.76 | 0.39 | 0.37 | 0.01 | 0.04 | 0.28 | 0.03 | 0.15 | 0.14 | 0.86 |
◊ȱ | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
X | 0.67 | 0.47 | 0.58 | 0.21 | 0.54 | 0.64 | 0.36 | 0.35 | 0.95 | 0.14 |
Y | 0.41 | 0.54 | 0.51 | 0.37 | 0.31 | 0.23 | 0.56 | 0.89 | 0.17 | 0.03 |
£®X∫ÕY∂º «0°´1÷ƺ‰µƒæ˘‘»Àʪ˙ ˝£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com