Question

【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且a2+c2=b2﹣ac．
（1）求B的大小；
（2）设∠BAC的平分线AD交BC于D，AD=2 ，BD=1，求cosC的值．

Answer 1

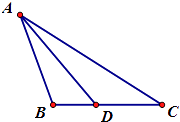
【答案】
（1）解：在△ABC中，∵a2+c2=b2﹣ac，即a2+c2﹣b2=﹣ac．

∴cosB= =﹣ =﹣ ，B∈（0，π），可得B= ．

（2）解：在△ABD中，由正弦定理可得： = ，

解得sin∠BAD= = ．

cos∠BAC=cos2∠BAD=1﹣2sin2∠BAD=1﹣×2× = ．

∴sin∠BAC= = = ．

∴cosC=cos（60°﹣∠BAC）= + = ．

【解析】（1）利用余弦定理可得：cosB=﹣ ，B∈（0，π），可得B．（2）在△ABD中，由正弦定理可得： = ，解得sin∠BAD．cos∠BAC=cos2∠BAD=1﹣2sin2∠BAD．可得sin∠BAC= ．可得cosC=cos（60°﹣∠BAC）．
【考点精析】本题主要考查了余弦定理的定义的相关知识点，需要掌握余弦定理:;;才能正确解答此题．