练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本题满分15分）甲、乙两人在罚球线投球命中的概率分别为，且各次投球相互之间没有影响．

    （1）甲、乙两人在罚球线各投球一次，求这二次投球中恰好命中一次的概率；

    （2）甲、乙两人在罚球线各投球二次，求这四次投球中至少有一次命中的概率．

    解：（1）依题意，记“甲投一次命中”为事件，“乙投一次命中”为事件，

    则， ，，．

    甲、乙两人在罚球线各投球一次，恰好命中一次的事件为

    =

    答：甲、乙两人在罚球线各投球一次，求恰好命中一次的概率为．………………8分

    （2）∵事件“甲、乙两人在罚球线各投球二次全不命中” 的概率是

    ……………………………………………………………… 12分

    ∴甲、乙两人在罚球线各投球二次，至少有一次命中的概率为 

    答：甲、乙两人在罚球线各投球二次,至少有一次命中的概率为…………………15分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

     

    19.（本题满分15分）甲乙两地相距km,汽车从甲地匀速驶到乙地，速度不得超过km/h,已知汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成，可变部分与速度km/h的平方成正比，比例系数为b,固定部分为a元. w.w.w.k.s.5.u.c.o.m         

    (1)把全程运输成本y（元）表示为(km/h)的函数，并指出这个函数的定义域；

    (2)为使全程运输成本最小，汽车应以多大速度行驶？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本题满分15分）已知5只动物中有1只患有某种疾病，需要通过化验血液来确定患病的动物．血液化验结果呈阳性的即为患病动物，呈阴性即没患病．下面是两种化验方法：

    方案甲：逐个化验，直到能确定患病动物为止．

    方案乙：先任取3只，将它们的血液混在一起化验．若结果呈阳性则表明患病动物为这3只中的1只，然后再逐个化验，直到能确定患病动物为止；若结果呈阴性则在另外2只中任取1只化验．

    （Ⅰ）分别求依方案甲所需化验次数与依方案乙所需化验次数的分布列；

    （Ⅱ）表示依方案乙所需化验次数，求的期望．。

    查看答案和解析>>

    科目：高中数学 来源：2010年江苏省高二第二学期期末考试数学（理）试题 题型：解答题

    （本题满分15分）甲、乙两人在罚球线投球命中的概率分别为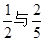，且各次投球相互之间没有影响．

    （1）甲、乙两人在罚球线各投球一次，求这二次投球中恰好命中一次的概率；

    （2）甲、乙两人在罚球线各投球二次，求这四次投球中至少有一次命中的概率．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本题满分15分）甲、乙两人在罚球线投球命中的概率分别为，且各次投球相互之间没有影响．

    （1）甲、乙两人在罚球线各投球一次，求这二次投球中恰好命中一次的概率；

    （2）甲、乙两人在罚球线各投球二次，求这四次投球中至少有一次命中的概率．

    查看答案和解析>>

    同步练习册答案