
【题目】如图,在平面四边形ABCD中,AD=1,CD=2,AC= ![]() .
. 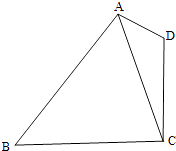
(1)求cos∠CAD的值;
(2)若cos∠BAD=﹣ ![]() ,sin∠CBA=
,sin∠CBA= ![]() ,求BC的长.
,求BC的长.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】椭圆 ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,右焦点到直线x+y+
,右焦点到直线x+y+ ![]() =0的距离为2
=0的距离为2 ![]() . (Ⅰ) 求椭圆的方程;
. (Ⅰ) 求椭圆的方程;
(Ⅱ) 过点M(0,﹣1)作直线l交椭圆于A,B两点,交x轴于N点,满足 ![]() =﹣
=﹣ ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连锁经营公司所属5个零售店某月的销售额利润资料如表:
商品名称 | A | B | C | D | E |
销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
(参考公式: ![]() =
=  =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() x)
x)
(1)画出销售额和利润额的散点图
(2)若销售额和利润额具有相关关系,试计算利润额y对销售额x的回归直线方程.
(3)估计要达到1000万元的利润额,销售额约为多少万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣1)|x﹣a|﹣x﹣2a(x∈R).
(1)若a=﹣1,求方程f(x)=1的解集;
(2)若 ![]() ,试判断函数y=f(x)在R上的零点个数,并求此时y=f(x)所有零点之和的取值范围.
,试判断函数y=f(x)在R上的零点个数,并求此时y=f(x)所有零点之和的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx+cos(x+ ![]() ),x∈R.
),x∈R.
(1)求f(x)的最小正周期及单调递增区间;
(2)若x是第二象限角,且f(x﹣ ![]() )=﹣
)=﹣ ![]() cos2x,求cosx﹣sinx的值.
cos2x,求cosx﹣sinx的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:函数f(x)=lg(ax2﹣x+ ![]() )的定义域为R;命题q:不等式3x﹣9x<a对一切正实数x均成立.如果“p或q”为真命题,“p且q”为假命题,求实数a的取值范围.
)的定义域为R;命题q:不等式3x﹣9x<a对一切正实数x均成立.如果“p或q”为真命题,“p且q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某航模兴趣小组的同学,为了测定在湖面上航模航行的速度,采用如下办法:在岸边设置两个观测点A,B(假设A,B,C,D在同一水平面上),且AB=80米,当航模在C 处时,测得∠ABC=
105°和∠BAC=30°,经过20秒后,航模直线航行到D 处,测得∠BAD=90°和∠ABD=45°.请你根据以上条件求出航模的速度.(答案保留根号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD= ![]() .用向量法解决下列问题:
.用向量法解决下列问题: 
(1)若AC的中点为E,求A1C与DE所成的角;
(2)求二面角B1﹣AC﹣D1(锐角)的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com