先后掷两个均匀正方体骰子(六个面分别标有点数1,2,3,4,5,6),骰子朝上的面的点数分别为X,Y,则log2XY=1的概率为多少?
【答案】
分析:根据题意,列举骰子朝上的面的点数的全部情况,可得其情况数目,再根据对数的运算性质,转化出X、Y之间的关系,可得满足log
2XY=1的情况数目,由等可能事件的概率,计算可得答案.
解答:解:掷两个均匀骰子,按骰子朝上的面的点数不同,共有36种情况,
分别为(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
6,1),(6,2),(6,3),(6,4),(6,5),(6,6),
要log
2XY=1,有2X=Y,其中X,Y∈{1,2,3,4,5,6}
满足条件的有(1,2),(2,4),(3,6);
则其概率为
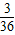
=
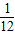
;
答:满足log
2XY=1的概率为
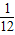
.
点评:本题考查列举法求古典概型,注意在列举事件基本情况时要做到不重不漏.

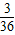 =
=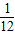 ;
;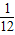 .
.
