
【题目】已知函数f(x)=x3﹣6x2+9x,g(x)= ![]() x3﹣
x3﹣ ![]() x2+ax﹣
x2+ax﹣ ![]() (a>1)若对任意的x1∈[0,4],总存在x2∈[0,4],使得f(x1)=g(x2),则实数a的取值范围为( )
(a>1)若对任意的x1∈[0,4],总存在x2∈[0,4],使得f(x1)=g(x2),则实数a的取值范围为( )
A.(1, ![]() ]??
]??
B.[9,+∞)??
C.(1, ![]() ]∪[9,+∞)??
]∪[9,+∞)??
D.[ ![]() ,
, ![]() ]∪[9,+∞)
]∪[9,+∞)
【答案】C
【解析】解:函数f(x)=x3﹣6x2+9x,导数为f′(x)=3x2﹣12x+9=3(x﹣1)(x﹣3), 可得f(x)的极值点为1,3,
由f(0)=0,f(1)=4,f(3)=0,f(4)=4,
可得f(x)在[0,4]的值域为[0,4];
g(x)= ![]() x3﹣
x3﹣ ![]() x2+ax﹣
x2+ax﹣ ![]() (a>1),
(a>1),
导数为g′(x)=x2﹣(a+1)x+a=(x﹣1)(x﹣a),
当1<x<a时,g′(x)<0,g(x)递减;
当x<1或x>a时,g′(x)>0,g(x)递增.
由g(0)=﹣ ![]() ,g(1)=
,g(1)= ![]() (a﹣1),g(a)=
(a﹣1),g(a)= ![]() a3﹣
a3﹣ ![]() a2﹣
a2﹣ ![]() >﹣
>﹣ ![]() ,g(4)=13﹣4a,
,g(4)=13﹣4a,
当3≤a≤4时,13﹣4a≤ ![]() (a﹣1),
(a﹣1),
g(x)在[0,4]的值域为[﹣ ![]() ,
, ![]() (a﹣1)],
(a﹣1)],
由对任意的x1∈[0,4],总存在x2∈[0,4],使得f(x1)=g(x2),
可得[0,4][﹣ ![]() ,
, ![]() (a﹣1)],
(a﹣1)],
即有4≤ ![]() (a﹣1),解得a≥9不成立;
(a﹣1),解得a≥9不成立;
当1<a<3时,13﹣4a> ![]() (a﹣1),
(a﹣1),
g(x)在[0,4]的值域为[﹣ ![]() ,13﹣4a],
,13﹣4a],
由题意可得[0,4][﹣ ![]() ,13﹣4a],
,13﹣4a],
即有4≤13﹣4a,解得a≤ ![]() ,即为1<a≤
,即为1<a≤ ![]() ;
;
当a>4时,可得g(1)取得最大值,g(4)<﹣3为最小值,
即有[0,4][13﹣4a, ![]() (a﹣1)],
(a﹣1)],
可得13﹣4a≤0,4≤ ![]() (a﹣1),即a≥
(a﹣1),即a≥ ![]() ]∪[9,+∞).
]∪[9,+∞).
故选:C.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】某车间20名工人年龄数据如表:
年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(Ⅰ) 求这20名工人年龄的众数与平均数;
(Ⅱ) 以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(Ⅲ) 从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(3,﹣1),|
=(3,﹣1),| ![]() |=
|= ![]() ,
, ![]() =﹣5,
=﹣5, ![]() =x
=x ![]() +(1﹣x)
+(1﹣x) ![]() .
.
(Ⅰ)若 ![]() ,求实数x的值;
,求实数x的值;
(Ⅱ)当| ![]() |取最小值时,求
|取最小值时,求 ![]() 与
与 ![]() 的夹角的余弦值.
的夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,锐角三角形ABC的内心为I,过点A作直线BI的垂线,垂足为H,点E为圆I与边CA的切点. 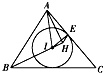
(1)求证A,I,H,E四点共圆;
(2)若∠C=50°,求∠IEH的度数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣1)ex+ax2有两个零点. (Ⅰ)求a的取值范围;
(Ⅱ)设x1 , x2是f(x)的两个零点,证明x1+x2<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,E是BC中点,M是PD上的中点,F是PC上的动点. (Ⅰ)求证:平面AEF⊥平面PAD
(Ⅱ)直线EM与平面PAD所成角的正切值为 ![]() ,当F是PC中点时,求二面角C﹣AF﹣E的余弦值.
,当F是PC中点时,求二面角C﹣AF﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)当a=0时,求f(x)在点(1,f(1))处的切线方程;
(2)是否存在实数a,当0<x≤2时,函数f(x)图象上的点都在 ![]() 所表示的平面区域(含边界)?若存在,求出a的值组成的集合;否则说明理由;
所表示的平面区域(含边界)?若存在,求出a的值组成的集合;否则说明理由;
(3)若f(x)有两个不同的极值点m,n(m>n),求过两点M(m,f(m)),N(n,f(n))的直线的斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com