
【题目】设函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() .
.
(![]() )求
)求![]() 的取值范围,并讨论
的取值范围,并讨论![]() 的单调性.
的单调性.
(![]() )证明:
)证明:![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析 : (1)先确定函数的定义域然后求导数![]() ,由题意知
,由题意知![]() ,
,![]() 是方程
是方程![]() 的两个均大于-1的不相等的实根,建立不等关系解之即可,在函数的定义域内解不等式
的两个均大于-1的不相等的实根,建立不等关系解之即可,在函数的定义域内解不等式![]() 和
和![]() ,求出单调区间;
,求出单调区间;
(2)![]() 是方程
是方程![]() 的根,将
的根,将![]() 用
用![]() 表示,消去
表示,消去![]() 得到关于
得到关于![]() 的函数,研究函数的单调性求出函数的最大值,即可证得不等式.
的函数,研究函数的单调性求出函数的最大值,即可证得不等式.
试题解析 :
(![]() )由题意知,函数
)由题意知,函数![]() 的定义域是
的定义域是![]() ,
,
![]() ,
,
且![]() 有两个不同的实数根
有两个不同的实数根![]() ,
,![]() ,故
,故![]() 的判别式
的判别式![]() ,即
,即![]() ,且
,且![]() ,
,![]() ,①
,①
又![]() ,故
,故![]() .因此
.因此![]() 的取值范围是
的取值范围是![]() .
.
当![]() 变化时
变化时![]() 与
与![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
因此![]() 在区间
在区间![]() 和
和![]() 是增函数,在
是增函数,在![]() 上是减函数.
上是减函数.
(![]() )由题意和①知,
)由题意和①知,![]() ,
,![]() ,
,
于是![]() .
.
设函数![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上是增函数.
上是增函数.
于是,当![]() ,
,![]() .因此
.因此![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知直线y=x+b与函数f(x)=ln x的图象交于两个不同的点A,B,其横坐标分别为x1,x2,且x1<x2.
(1)求b的取值范围;
(2)当x2≥2时,证明x1·![]() <2.
<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018湖北七市(州)教研协作体3月高三联考】已知椭圆![]() :
: ![]()
![]() 的左顶点为
的左顶点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 与直线
与直线![]() 垂直,垂足为
垂直,垂足为![]() 点,且点
点,且点![]() 是线段
是线段![]() 的中点.
的中点.
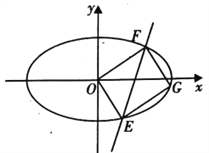
(I)求椭圆![]() 的方程;
的方程;
(II)如图,若直线![]() :
: ![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,点
两点,点![]() 在椭圆
在椭圆![]() 上,且四边形
上,且四边形![]() 为平行四边形,求证:四边形
为平行四边形,求证:四边形![]() 的面积
的面积![]() 为定值.
为定值.
【答案】(I)![]() ;(II)
;(II)![]()
【解析】试题分析:(1)根据题意可得![]() ,
, ![]() 故斜率为
故斜率为![]() ,由直线
,由直线![]() 与直线
与直线![]() 垂直,可得
垂直,可得![]() ,因为点
,因为点![]() 是线段
是线段![]() 的中点,∴点
的中点,∴点![]() 的坐标是
的坐标是![]() ,
,
代入直线得![]() ,连立方程即可得
,连立方程即可得![]() ,
, ![]() ;(2)∵四边形
;(2)∵四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,设
,设![]() ,
, ![]() ,
, ![]() ,∴
,∴![]()
![]() ,得
,得![]() ,将
,将![]() 点坐标代入椭圆
点坐标代入椭圆![]() 方程得
方程得![]() ,
,
点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,利用弦长公式得EF,则平行四边形
,利用弦长公式得EF,则平行四边形![]() 的面积为
的面积为
![]()
![]()
![]()
![]()
![]()
![]() .
.
解析:(1)由题意知,椭圆![]() 的左顶点
的左顶点![]() ,上顶点
,上顶点![]() ,直线
,直线![]() 的斜率
的斜率![]() ,
,
得![]() ,
,
因为点![]() 是线段
是线段![]() 的中点,∴点
的中点,∴点![]() 的坐标是
的坐标是![]() ,
,
由点![]() 在直线
在直线![]() 上,∴
上,∴![]() ,且
,且![]() ,
,
解得![]() ,
, ![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,
, ![]() ,
, ![]() ,
,
将![]() 代入
代入![]() 消去
消去![]() 并整理得
并整理得![]()
![]() ,
,
则![]() ,
, ![]() ,
,
![]()
![]() ,
,
∵四边形![]() 为平行四边形,∴
为平行四边形,∴![]()
![]() ,
,
得![]() ,将
,将![]() 点坐标代入椭圆
点坐标代入椭圆![]() 方程得
方程得![]() ,
,
点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
, ![]() ,
,
∴平行四边形![]() 的面积为
的面积为
![]()
![]()
![]()
![]()
![]()
![]() .
.
故平行四边形![]() 的面积
的面积![]() 为定值
为定值![]() .
.
【题型】解答题
【结束】
21
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,求证:函数
时,求证:函数![]() 有两个不相等的零点
有两个不相等的零点![]() ,
, ![]() ,且
,且![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴正方向建立平面直角坐标系,曲线
轴正方向建立平面直角坐标系,曲线![]() 的直角坐标方程是
的直角坐标方程是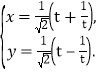 (
(![]() 为参数).
为参数).
(Ⅰ)将曲线![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)求曲线![]() 与曲线
与曲线![]() 交点的极坐标.
交点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 上的两个点,点
上的两个点,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .设抛物线
.设抛物线![]() 的焦点在直线
的焦点在直线![]() 的下方.
的下方.
(Ⅰ)求k的取值范围;
(Ⅱ)设C为W上一点,且![]() ,过
,过![]() 两点分别作W的切线,记两切线的交点为
两点分别作W的切线,记两切线的交点为![]() . 判断四边形
. 判断四边形![]() 是否为梯形,并说明理由.
是否为梯形,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为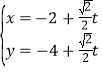 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳(单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则
(A)2号学生进入30秒跳绳决赛
(B)5号学生进入30秒跳绳决赛
(C)8号学生进入30秒跳绳决赛
(D)9号学生进入30秒跳绳决赛
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com