
 =
=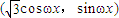 ,
,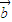 =(sinωx,0),其中ω>0,记函数f(x)=(
=(sinωx,0),其中ω>0,记函数f(x)=(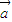 +
+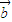 )•
)•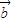 +k.
+k. ,求ω的取值范围.
,求ω的取值范围.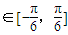 时,f(x)的最大值是
时,f(x)的最大值是 ,求f(x)的解析式,并说明如何由y=sinx的图象变换得到y=f(x)的图象.
,求f(x)的解析式,并说明如何由y=sinx的图象变换得到y=f(x)的图象. ,得到关系式,求出ω的取值范围;
,得到关系式,求出ω的取值范围; =(
=( cosωx,sinωx),
cosωx,sinωx), =(sinωx,0),
=(sinωx,0), +
+ =(
=( cosωx+sinωx,sinωx).
cosωx+sinωx,sinωx). +
+ )•
)• +k=
+k= sinωxcosωx+sin2ωx+k
sinωxcosωx+sin2ωx+k sin2ωx+
sin2ωx+ +k=
+k= sin2ωx-
sin2ωx- cos2ωx+
cos2ωx+ +k
+k )+k+
)+k+ .
. =
= ≥
≥ ,∴ω≤1.
,∴ω≤1. =π,∴ω=1.
=π,∴ω=1. )+k+
)+k+ .
. ,
, ],∴2x-
],∴2x- ∈[-
∈[- ,
, ].
]. =
= ,即x=
,即x= 时,f(x)max=f(
时,f(x)max=f( )=sin
)=sin +k+
+k+ =k+1=
=k+1= ,
, .故f(x)=sin(2x-
.故f(x)=sin(2x- ).
). 个单位长度,得到函数y=sin(x-
个单位长度,得到函数y=sin(x- )的图象,再将得到的函数图象上所有点的横坐标变为原来的
)的图象,再将得到的函数图象上所有点的横坐标变为原来的 倍(纵坐标不变),得到函数y=sin(2x-
倍(纵坐标不变),得到函数y=sin(2x- )的图象.
)的图象.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源:101网校同步练习 高一数学 人教社(新课标B 2004年初审通过) 人教实验版 题型:013
若3sinx-![]() cosx=
cosx=![]() sin(x+
sin(x+![]() ),
),![]() ∈(-π,π),则
∈(-π,π),则![]() 等于
等于
A.-![]()
B.![]()
C.![]()
D.-![]()
查看答案和解析>>
科目:高中数学 来源: 题型:044
(2006
江西九校模拟)已知向量 ,n=(cos x,cos x),
,n=(cos x,cos x), .
.
(1)
若m∥p,求sin x·cos x的值;(2)
设△ABC的三边a、b、c满足 ,且边b所对的角θ的取值集合为M.当
,且边b所对的角θ的取值集合为M.当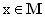 时,求函数f(x)=m·n的值域.
时,求函数f(x)=m·n的值域.查看答案和解析>>
科目:高中数学 来源:湖北省八市2012届高三3月联考数学文科试题 题型:022
若将函数y=sin(ωx+![]() )(ω>0)的图象向右平移
)(ω>0)的图象向右平移![]() 个单位长度后,与函数y=sin(ωx+
个单位长度后,与函数y=sin(ωx+![]() )的图象重合,则ω的最小值为________.
)的图象重合,则ω的最小值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com