
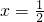 有无数多个解;
有无数多个解; 解:∵函数{x}的定义域为R,又∵{x+1}=(x+1)-[x+1]=x-[x]={x},
解:∵函数{x}的定义域为R,又∵{x+1}=(x+1)-[x+1]=x-[x]={x}, 时,{x}=
时,{x}= ,又∵函数{x}=x-[x]是周期为1的函数,∴x=
,又∵函数{x}=x-[x]是周期为1的函数,∴x= +k时(k∈Z),{x}=
+k时(k∈Z),{x}= ∴②是正确的,
∴②是正确的,

科目:高中数学 来源: 题型:
| 5 |
| 4 |
| C | x n |
| n(n-1)(n-2)…(n-[x]+1) |
| x(x-1)…(x-[x]+1) |
| C |
8 |
| 16 |
| 3 |
| 16 |
| 3 |
| C | x 8 |
| 28 |
| 3 |
| 28 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年湖南卷文)设![]() 表示不超x的最大整数,(如
表示不超x的最大整数,(如![]() )。对于给定的
)。对于给定的![]() ,定义
,定义![]() 则
则![]() ________;
________;
当![]() 时,函数
时,函数![]() 的值域是_________________________。
的值域是_________________________。
查看答案和解析>>
科目:高中数学 来源: 题型:
(湖南卷文15)设![]() 表示不超x的最大整数,(如
表示不超x的最大整数,(如![]() )。对于给定的
)。对于给定的![]() ,
,
定义![]() 则
则![]() ________;当
________;当![]() 时,函数
时,函数![]() 的值域是_________________________。
的值域是_________________________。
查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校校招生全国统一考试数学文史类(湖南卷) 题型:填空题
设 表示不超x的最大整数,(如
表示不超x的最大整数,(如 )。对于给定的
)。对于给定的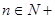 ,
,
定义 则
则 ________;
________;
当 时,函数
时,函数 的值域是_________________________。
的值域是_________________________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com