
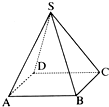
 正棱锥S-ABCD的底面边长为4,高为1,求:
正棱锥S-ABCD的底面边长为4,高为1,求:分析 (1)设SO为正四棱锥S-ABCD的高,则SO=1,作OM⊥BC,则M为BC 中点,连结OM,OB,则SO⊥OB,SO⊥OM,由此能求出棱锥的侧棱长和斜高.
(2)棱锥的表面积S=S正方形ABCD+4S△SBC,由此能求出结果.
解答 解:(1)设SO为正四棱锥S-ABCD的高,则SO=1,
作OM⊥BC,则M为BC 中点,
连结OM,OB,则SO⊥OB,SO⊥OM,
BC=4,BM=2,则OM=2,OB=2$\sqrt{2}$,
在Rt△SOD中,SB=$\sqrt{S{O}^{2}+O{B}^{2}}$=$\sqrt{1+8}=3$,
在Rt△SOM中,SM=$\sqrt{5}$,
∴棱锥的侧棱长为3,斜高为$\sqrt{5}$.
(2)棱锥的表面积:
S=S正方形ABCD+4S△SBC
=$4×4+4×(\frac{1}{2}×4×\sqrt{5})$
=16+8$\sqrt{5}$.
点评 本题考查棱锥的侧棱长和斜高及棱锥的表面积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:解答题
 设函数f(x)=sin(ωx+φ)(ω>0,-π<φ<0)的两个相邻的对称中心分别为(${\frac{π}{8}$,0),(${\frac{5π}{8}$,0).
设函数f(x)=sin(ωx+φ)(ω>0,-π<φ<0)的两个相邻的对称中心分别为(${\frac{π}{8}$,0),(${\frac{5π}{8}$,0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在某次测量中得到的A样本的茎叶图如图所示,则该样本的中位数、众数、极差分别是( )
在某次测量中得到的A样本的茎叶图如图所示,则该样本的中位数、众数、极差分别是( )| A. | 47,45,56 | B. | 46,45,53 | C. | 45,47,53 | D. | 46,45,56 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i | B. | -i | C. | $\sqrt{3}$+i | D. | $\sqrt{3}$-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{9}$=1(y≠0) | B. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1(y≠0) | ||
| C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1(y≠0) | D. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{16}$=1(y≠0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知四棱锥P-ABCD,底面ABCD为菱形,△PAB是等边三角形,∠ABC=60°,AB=2,PC=$\sqrt{6}$
已知四棱锥P-ABCD,底面ABCD为菱形,△PAB是等边三角形,∠ABC=60°,AB=2,PC=$\sqrt{6}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com