
已知函数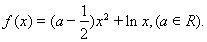
(Ⅰ)当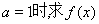 在区间
在区间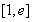 上的最大值和最小值;
上的最大值和最小值;
(Ⅱ)若在区间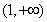 上,函数
上,函数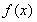 的图象恒在直线
的图象恒在直线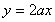 下方,求
下方,求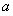 的取值范围.
的取值范围.
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十二第十章第九节练习卷(解析版) 题型:解答题
甲、乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如下:
甲运动员
射击环数 | 频数 | 频率 |
7 | 10 | 0.1 |
8 | 10 | 0.1 |
9 | x | 0.45 |
10 | 35 | y |
合计 | 100 | 1 |
乙运动员
射击环数 | 频数 | 频率 |
7 | 8 | 0.1 |
8 | 12 | 0.15 |
9 | z |
|
10 |
| 0.35 |
合计 | 80 | 1 |
若将频率视为概率,回答下列问题:
(1)求甲运动员射击1次击中10环的概率.
(2)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率.
(3)若甲运动员射击2次,乙运动员射击1次,ξ表示这3次射击中击中9环以上(含9环)的次数,求ξ的分布列及E(ξ).
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数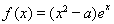 .
.
(Ⅰ)若函数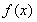 在
在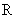 上不是单调函数,求实数
上不是单调函数,求实数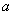 的取值范围;
的取值范围;
(Ⅱ)当 时,讨论函数
时,讨论函数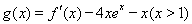 的零点个数.
的零点个数.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数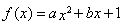 在
在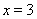 处的切线方程为
处的切线方程为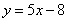 .
.
(1)求函数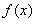 的解析式;
的解析式;
(2)若关于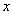 的方程
的方程 恰有两个不同的实根,求实数
恰有两个不同的实根,求实数 的值;
的值;
(3)数列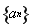 满足
满足 ,
,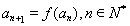 ,求
,求 的整数部分.
的整数部分.
查看答案和解析>>
科目:高中数学 来源:2014年高中数学全国各省市理科导数精选22道大题练习卷(解析版) 题型:解答题
已知函数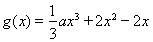 ,函数
,函数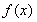 是函数
是函数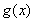 的导函数.
的导函数.
(1)若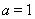 ,求
,求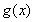 的单调减区间;
的单调减区间;
(2)若对任意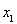 ,
,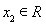 且
且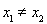 ,都有
,都有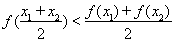 ,求实数
,求实数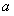 的取值范围;
的取值范围;
(3)在第(2)问求出的实数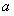 的范围内,若存在一个与
的范围内,若存在一个与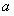 有关的负数
有关的负数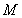 ,使得对任意
,使得对任意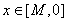 时
时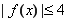 恒成立,求
恒成立,求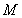 的最小值及相应的
的最小值及相应的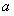 值.
值.
查看答案和解析>>
科目:高中数学 来源:2014年陕西省咸阳市高考模拟考试(一)理科数学试卷(解析版) 题型:解答题
已知函数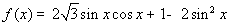 ,x?R.
,x?R.
(1)求函数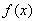 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)将函数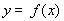 的图象上各点的纵坐标保持不变,横坐标先缩短到原来的
的图象上各点的纵坐标保持不变,横坐标先缩短到原来的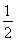 ,把所得到的图象再向左平移
,把所得到的图象再向左平移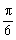 单位,得到函数
单位,得到函数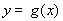 的图象,求函数
的图象,求函数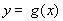 在区间
在区间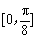 上的最小值.
上的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com