
【题目】已知函数![]() (a>0).
(a>0).
(1)讨论函数f(x)的单调性;
(2)证明:对任意x∈[1,+∞),有f(x)≤2x-a2.
【答案】(1)详见解析(2)详见解析
【解析】
(1)对函数求导,分情况讨论导函数的正负,进而得到单调区间;(2)构造函数![]() ,对函数求导,研究函数的单调性,得到函数的最值,证明函数的最大值小于0即可.
,对函数求导,研究函数的单调性,得到函数的最值,证明函数的最大值小于0即可.
(1)解: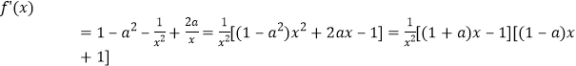 .
.
①当0<a≤1时,由f'(x)<0,得[(1+a)x-1][(1-a)x+1]<0,
解得![]() ;
;
由f'(x)>0,得[(1+a)x-1][(1-a)x+1]>0,解得![]() .
.
故函数f(x)的单调递减区间为(0,![]() ),单调递增区间为(
),单调递增区间为(![]() ,+∞).
,+∞).
②当a>1时,由f'(x)<0,得![]() 或
或![]() ;
;
由f'(x)>0,得![]() .
.
故函数f(x)的单调递减区间为(0,![]() ),(
),(![]() ,+∞),单调递增区间为
,+∞),单调递增区间为![]() .
.
(2)证明:构造函数![]() ,
,
则![]() .
.
因为Δ=(2a)2-4(1+a2)<0,
所以(1+a2)x2-2ax+1>0,即g'(x)<0.
故g(x)在区间[1,+∞)上是减函数.
又x≥1,所以g(x)≤g(1)=-(1+a2)+1+a2=0.
故对任意x∈[1,+∞),有f(x)≤2x-a2.


科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并求出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABCA1B1C1中,BC=BB1,∠BAC=∠BCA=![]() ∠ABC,点E是A1B与AB1的交点,点D在线段AC上,B1C∥平面A1BD.
∠ABC,点E是A1B与AB1的交点,点D在线段AC上,B1C∥平面A1BD.
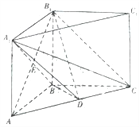
(1)求证:BD⊥A1C;
(2)求证:AB1⊥平面A1BC。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国务院批准从2009年起,将每年8月8日设置为“全民健身日”,为响应国家号召,各地利用已有土地资源建设健身场所.如图,有一个长方形地块![]() ,边
,边![]() 为
为![]() ,
,![]() 为
为![]() .地块的一角是草坪(图中阴影部分),其边缘线
.地块的一角是草坪(图中阴影部分),其边缘线![]() 是以直线
是以直线![]() 为对称轴,以
为对称轴,以![]() 为顶点的抛物线的一部分.现要铺设一条过边缘线
为顶点的抛物线的一部分.现要铺设一条过边缘线![]() 上一点
上一点![]() 的直线型隔离带
的直线型隔离带![]() ,
,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上(隔离带不能穿越草坪,且占地面积忽略不计),将隔离出的
上(隔离带不能穿越草坪,且占地面积忽略不计),将隔离出的![]() 作为健身场所.则
作为健身场所.则![]() 的面积为
的面积为![]() 的最大值为____________(单位:
的最大值为____________(单位:![]() ).
).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)试探究函数![]() 在定义域内是否存在零点,若存在,请指出有几个零点;若不存在,请说明理由;
在定义域内是否存在零点,若存在,请指出有几个零点;若不存在,请说明理由;
(Ⅲ)若![]() ,且
,且![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计:
(万元)有如下统计:
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
. 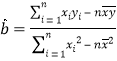 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2)![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的部分图象如图所示.
的部分图象如图所示.
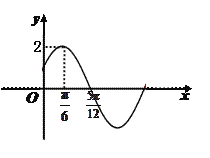
(1) 求函数![]() 的解析式;
的解析式;
(2) 如何由函数![]() 的通过适当图象的变换得到函数
的通过适当图象的变换得到函数![]() 的图象, 写出变换过程;
的图象, 写出变换过程;
(3) 若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图像可以由y=cos2x的图像先纵坐标不变横坐标伸长到原来的2倍,再横坐标不变纵坐标伸长到原来的2倍,最后向右平移![]() 个单位而得到.
个单位而得到.
⑴求f(x)的解析式与最小正周期;
⑵求f(x)在x∈(0,π)上的值域与单调性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com