
【题目】已知0<m<2,动点M到两定点F1(﹣m,0),F2(m,0)的距离之和为4,设点M的轨迹为曲线C,若曲线C过点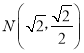 .
.
(1)求m的值以及曲线C的方程;
(2)过定点![]() 且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
【答案】(1)![]() ,
, ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据椭圆的定义可知曲线C是以两定点F1,F2为焦点,长半轴长为2的椭圆,再代入点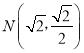 求得椭圆中的基本量即可.
求得椭圆中的基本量即可.
(2)设直线![]() ,再联立椭圆的方程,得出韦达定理,代入
,再联立椭圆的方程,得出韦达定理,代入![]() 进行计算可得
进行计算可得![]() 证明即可.
证明即可.
(1)解:设M(x,y),因为|MF1|+|MF2|=4>2m,所以曲线C是以两定点F1,F2为焦点,长半轴长为2的椭圆,所以a=2.
设椭圆C的方程为![]() 1(b>0),代入点
1(b>0),代入点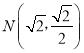 得b2=1,
得b2=1,
由c2=a2﹣b2,得c2=3,
所以![]() ,故曲线C的方程为
,故曲线C的方程为![]() ;
;
(2)证明:设直线l:x=ty![]() ,A(x1,y1),B(x2,y2),
,A(x1,y1),B(x2,y2),
椭圆的右顶点为P(2,0),联立方程组
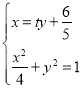 消去x得
消去x得![]() 0.
0.
△>0,y1+y2 ,y1y2
,y1y2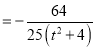 ,
,
所以![]()
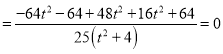 ,∴
,∴![]() ,
,
故点P在以AB为直径的圆上,即以AB为直径的圆过曲线C的右顶点.


科目:高中数学 来源: 题型:
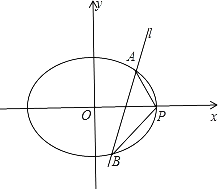
【题目】已知椭圆![]() :
:![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,左顶点为
,左顶点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过原点![]() 且与
且与![]() 轴不重合的直线交椭圆
轴不重合的直线交椭圆![]() 于
于![]() ,
,![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
,![]() ,.求证:以
,.求证:以![]() 为直径的圆恒过交点
为直径的圆恒过交点![]() ,
,![]() ,并求出
,并求出![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△ABC中,AB⊥BC,∠ACB=60°,D为AC中点,△ABD沿BD翻折过程中,直线AB与直线BC所成的最大角、最小角分别记为α1,β1,直线AD与直线BC所成最大角、最小角分别记为α2,β2,则有( )
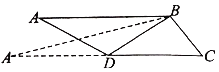
A.α1<α2,β1≤β2B.α1<α2,β1>β2
C.α1≥α2,β1≤β2D.α1≥α2,β1>β2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司对旗下的甲、乙两个门店在1至9月份的营业额(单位:万元)进行统计并得到如图折线图.
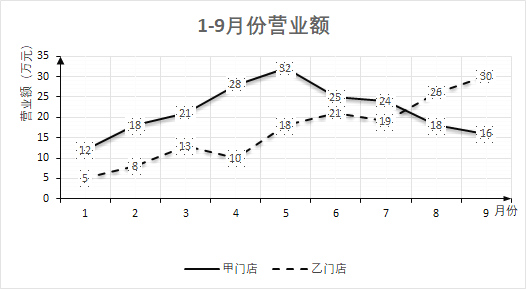
下面关于两个门店营业额的分析中,错误的是( )
A.甲门店的营业额折线图具有较好的对称性,故而营业额的平均值约为32万元
B.根据甲门店的营业额折线图可知,该门店营业额的平均值在[20,25]内
C.根据乙门店的营业额折线图可知,其营业额总体是上升趋势
D.乙门店在这9个月份中的营业额的极差为25万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F是椭圆![]() 的左焦点,过点F且斜率为正的直线与E相交于A、B两点,过点A、B分别作直线AM和BN满足AM⊥l,BN⊥l,且直线AM、BN分别与x轴相交于M和N.试求|MN|的最小值.
的左焦点,过点F且斜率为正的直线与E相交于A、B两点,过点A、B分别作直线AM和BN满足AM⊥l,BN⊥l,且直线AM、BN分别与x轴相交于M和N.试求|MN|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述中错误的是( )
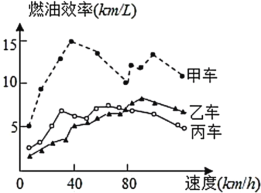
A.消耗1升汽油乙车最多可行驶5千米.
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多.
C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油.
D.某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱台![]() 的下底面
的下底面![]() 是边长为2的正三角形,上地面
是边长为2的正三角形,上地面![]() 是边长为1的正三角形.
是边长为1的正三角形.![]() 在下底面的射影为
在下底面的射影为![]() 的重心,且
的重心,且![]() .
.
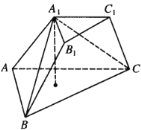
(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() 的离心率为
的离心率为![]() ,其右焦点到椭圆C外一点
,其右焦点到椭圆C外一点![]() 的距离为
的距离为![]() ,不过原点O的直线l与椭圆C相交于A,B两点,且线段AB的长度为2.
,不过原点O的直线l与椭圆C相交于A,B两点,且线段AB的长度为2.
![]() 1
1![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 2
2![]() 求
求![]() 面积S的最大值.
面积S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com