
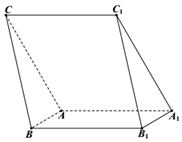
 如图,三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面ABB1A1,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=1.
如图,三棱柱ABC-A1B1C1中,侧面ACC1A1⊥侧面ABB1A1,∠B1A1A=∠C1A1A=60°,AA1=AC=4,AB=1.分析 (Ⅰ)取AA1中点O,连结OC1,AC1,推导出OC1⊥AA1,OC1⊥A1B1,A1B1⊥OB1,从而A1B1⊥平面OB1C1,由此能证明A1B1⊥B1C1.
(Ⅱ)在平行四边形ABB1A1中,过B1作B1E⊥1于点E,过O作OF⊥BB1于点F,则OFB1E为矩形推导出BB1⊥OC1,C1F⊥BB1,由此能求出三棱锥ABC-A1B1C1的侧面积.
解答 证明:(Ⅰ)取AA1中点O,连结OC1,AC1,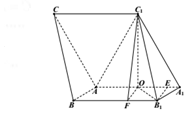
∵AA1=AC=A1C1=4,∠C1A1A=60°,∴△AC1A1为正三角形,
∴OC1⊥AA1,OC1=2$\sqrt{3}$,
又侧面ACC1A1⊥侧面ABB1A1,面ACC1A1∩面ABB1A1=AA1,OC1?面ACC1A1,
∴OC1⊥平面ABB1A1,
又A1B1?平面ABB1A1,∴OC1⊥A1B1,
在△OA1B1中,∵∠OA1B1=60°,A1B1=AB=1,OA1=2,
∴$O{{B}_{1}}^{2}$=1+4-2×1×2×cos60°=3,解得OB1=$\sqrt{3}$,
∴OA12=OB12+${A}_{1}{{B}_{1}}^{2}$,∴A1B1⊥OB1,
又OB1∩OC1=O,OB1?平面OB1C1,OC1?平面OB1C1,
∴A1B1⊥平面OB1C1,
∵B1C1?平面OB1C1,∴A1B1⊥B1C1.
解:(Ⅱ)依题意,${S}_{AB{B}_{1}{A}_{1}}=2×\frac{1}{2}×{A}_{1}{B}_{1}×A{A}_{1}×sin60°$=8$\sqrt{3}$,
在平行四边形ABB1A1中,过B1作B1E⊥1于点E,
过O作OF⊥BB1于点F,则OFB1E为矩形,∴OF=B1E,
由(1)知OC1⊥平面ABB1A1,BB1?平面ABB1A1,
∴BB1⊥OC1,
∵BB1⊥OF,OC1∩OF=O,OC1?平面OC1F,OF?平面OC1F,
∴BB1⊥平面OC1F,∵C1F?平面OC1F,
∴C1F⊥BB1,
∵${B}_{1}E={A}_{1}{B}_{1}•sin60°=\frac{\sqrt{3}}{2}$,
在Rt△OC1F中,OC1=2$\sqrt{3}$,OF=B1E=$\frac{\sqrt{3}}{2}$,
∴C1F=$\sqrt{(2\sqrt{3})^{2}+(\frac{\sqrt{3}}{2})^{2}}$=$\frac{\sqrt{51}}{2}$,
∴${S}_{BC{C}_{1}{B}_{1}}$=BB1×${C}_{1}F=2\sqrt{51}$,
∴三棱锥ABC-A1B1C1的侧面积S=2$\sqrt{3}+8\sqrt{3}+2\sqrt{51}$=$10\sqrt{3}+2\sqrt{51}$.
点评 本题考查线线垂直的证明,考查三棱锥的侧面积的求法,考查直线与直线、直线与平面、平面与平面的位置关系等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查化归与转化思想,是中档题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{4}{3}$,4] | B. | [$\frac{4}{3}$,4) | C. | [2,4] | D. | (2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | $4\sqrt{2}$ | C. | 6 | D. | $2\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,则$\overrightarrow{b}$=$\overrightarrow{c}$ | B. | 若$\overrightarrow{a}$=(1,k),$\overrightarrow{b}$=(-2,6),$\overrightarrow{a}$∥$\overrightarrow{b}$,则k=$\frac{1}{3}$ | ||
| C. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow{a}$•$\overrightarrow{b}$=0 | D. | 若$\overrightarrow{a}$与$\overrightarrow{b}$是单位向量,则$\overrightarrow{a}$•$\overrightarrow{b}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | [-$\sqrt{2}$,$\sqrt{6}$] | C. | [-$\sqrt{6}$,$\sqrt{6}$] | D. | [-$\sqrt{6}$,$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<2} | B. | {x|0<x<1} | C. | {x|0≤x<1} | D. | {x|-1<x<0} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com