
分析 根据题意得出f(0)=0,-2≤x<0时,f(x)>0,0<x≤2时,f(x)<0;
把不等式xf(2x-1)<0化为等价的不等式组,求出它的解集即可.
解答 解:∵f(x)是奇函数,且在[-2,2]内是单调减函数,
∴f(0)=0,
且当-2≤x<0时,f(x)>0,
0<x≤2时,f(x)<0;
∴不等式xf(2x-1)<0等价于
$\left\{\begin{array}{l}{-2≤x<0}\\{-2≤2x-1<0}\end{array}\right.$或$\left\{\begin{array}{l}{0<x≤2}\\{0<2x-1≤2}\end{array}\right.$,
解得-$\frac{1}{2}$≤x<$\frac{1}{2}$或$\frac{1}{2}$<x≤$\frac{3}{2}$;
∴该不等式的解集为[-$\frac{1}{2}$,$\frac{1}{2}$)∪($\frac{1}{2}$,$\frac{3}{2}$].
点评 本题考查了函数的奇偶性与单调性的应用问题,也考查了转化思想的应用问题,是基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数f(x)=2sin(2x+$\frac{π}{6}$)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列判断错误的是( )
已知函数f(x)=2sin(2x+$\frac{π}{6}$)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则下列判断错误的是( )| A. | ω=2 | |
| B. | f($\frac{π}{3}$)=1 | |
| C. | 函数f(x)的图象关于(-$\frac{11π}{12}$,0)对称 | |
| D. | 函数f(x)的图象向右平移$\frac{π}{12}$个单位后得到y=Asinωx的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (1,2) | D. | (2,3) |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北冀州市高二文上月考三数学试卷(解析版) 题型:解答题
如图,已知定圆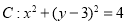 ,定直线
,定直线 ,过
,过 的一条动直线
的一条动直线 与直线相交于
与直线相交于 ,与圆
,与圆 相交于
相交于 ,
, 两点,
两点, 是
是 中点.
中点.
(Ⅰ)当 与
与 垂直时,求证:
垂直时,求证: 过圆心
过圆心 ;
;
(Ⅱ)当 时,求直线
时,求直线 的方程;
的方程;
(Ⅲ)设 ,试问
,试问 是否为定值,若为定值,请求出
是否为定值,若为定值,请求出 的值;若不为定值,请说明理由.
的值;若不为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广西陆川县中学高二理9月月考数学试卷(解析版) 题型:选择题
在锐角 中,
中, 分别为角
分别为角 所对的边,满足
所对的边,满足 ,且
,且 的面积
的面积 ,则
,则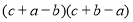 的取值范围是( )
的取值范围是( )
A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com