
【题目】在多面体![]() 中,底面
中,底面![]() 是梯形,四边形
是梯形,四边形![]() 是正方形,
是正方形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,

(1)求证:平面![]() 平面
平面![]() ;
;
(2)设![]() 为线段
为线段![]() 上一点,
上一点,![]() ,求二面角
,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)见解析;(2)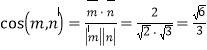 .
.
【解析】分析:(1)由勾股定理的逆定理可得![]() ,
,![]() ;又由条件可得到
;又由条件可得到![]() ,于是
,于是![]() 平面
平面![]() ,可得
,可得![]() ,从而得到
,从而得到![]() 平面
平面![]() ,根据面面垂直的判定定理得平面
,根据面面垂直的判定定理得平面![]() 平面
平面![]() .(2)由题意得可得
.(2)由题意得可得![]() ,
,![]() ,
,![]() 两两垂直,故可建立空间直角坐标系,结合题意可得点
两两垂直,故可建立空间直角坐标系,结合题意可得点![]() ,于是可求得平面
,于是可求得平面![]() 的法向量为
的法向量为![]() ,又
,又![]() 是平面
是平面![]() 的一个法向量,求得
的一个法向量,求得![]() 后结合图形可得所求余弦值为
后结合图形可得所求余弦值为![]() .
.
详解:(1)由![]() ,
,![]() ,
,![]() ,得
,得![]() ,
,
∴![]() 为直角三角形,且
为直角三角形,且![]()
同理![]() 为直角三角形,且
为直角三角形,且![]() .
.
又四边形![]() 是正方形,
是正方形,
∴![]() .
.
又![]()
∴![]() .
.
在梯形![]() 中,过点作
中,过点作![]() 作
作![]() 于
于![]() ,
,
故四边形![]() 是正方形,
是正方形,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)由(1)可得![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() ,
,
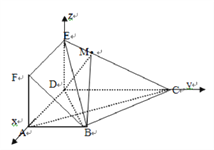
则![]() .
.
令![]() ,则
,则![]() ,
,![]()
∵![]() ,
,
∴![]()
∴点![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
设平面![]() 的法向量为
的法向量为![]() .
.
则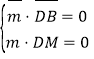 ,即
,即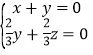 ,可得
,可得![]() .
.
令![]() ,得
,得![]() .
.
∴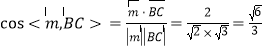 .
.
由图形知二面角![]() 为锐角,
为锐角,
∴二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,抛物线关于![]() 轴对称,它的顶点在坐标原点,点
轴对称,它的顶点在坐标原点,点![]() 、
、![]() 、
、![]() 均在抛物线上.
均在抛物线上.
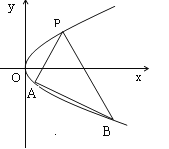
(1)写出该抛物线的方程及其准线方程;
(2)当![]() 与
与![]() 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求![]() 的值及直线
的值及直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)求![]() 在区间
在区间![]() 上的最小值.
上的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】(Ⅰ)![]() .
.
令![]() ,得
,得![]() .
.

![]() 与
与![]() 的情况如上:
的情况如上:
所以,![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
(Ⅱ)当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
当![]() ,即
,即![]() 时,
时,
由(Ⅰ)知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
综上,当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
【题型】解答题
【结束】
19
【题目】已知抛物线![]() 的顶点在原点,焦点在坐标轴上,点
的顶点在原点,焦点在坐标轴上,点![]() 为抛物线
为抛物线![]() 上一点.
上一点.
(1)求![]() 的方程;
的方程;
(2)若点![]() 在
在![]() 上,过
上,过![]() 作
作![]() 的两弦
的两弦![]() 与
与![]() ,若
,若![]() ,求证: 直线
,求证: 直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}和{bn}满足,a1=2,b1=1,且对任意正整数n恒满足2an+1=4an+2bn+1,2bn+1=2an+4bn﹣1.
(1)求证:{an+bn}为等比数列,{an﹣bn}为等差列;
(2)求证![]() (n>1).
(n>1).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两焦点为
的两焦点为![]() ,
, ![]() ,
, ![]() 为椭圆上一点,且到两个焦点的距离之和为6.
为椭圆上一点,且到两个焦点的距离之和为6.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若已知直线![]() ,当
,当![]() 为何值时,直线与椭圆
为何值时,直线与椭圆![]() 有公共点?
有公共点?
(3)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按文献记载,《百家姓》成文于北宋初年,表1记录了《百家姓》开头的24大姓氏:
表1:
赵 | 钱 | 孙 | 李 | 周 | 吴 | 郑 | 王 | 冯 | 陈 | 褚 | 卫 |
蒋 | 沈 | 韩 | 杨 | 朱 | 秦 | 尤 | 许 | 何 | 吕 | 施 | 张 |
表2记录了2018年中国人口最多的前10大姓氏:
表2:
1:李 | 2:王 | 3:张 | 4:刘 | 5:陈 |
6:杨 | 7:赵 | 8:黄 | 9:周 | 10:吴 |
从《百家姓》开头的24大姓氏中随机选取1个姓氏,则这个姓氏是2018年中国人口最多的前10大姓氏的概率为_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com