
【题目】阅读下列材料,回答所提问题:设函数![]() ,①
,①![]() 的定义域为
的定义域为![]() ,其图像是一条连续不断的曲线;②
,其图像是一条连续不断的曲线;②![]() 是偶函数;③
是偶函数;③![]() 在
在![]() 上不是单调函数;④
上不是单调函数;④![]() 恰有
恰有![]() 个零点,写出符合上述①②④条件的一个函数的解析式是______;写出符合上述所有条件的一个函数的解析式是______.
个零点,写出符合上述①②④条件的一个函数的解析式是______;写出符合上述所有条件的一个函数的解析式是______.
【答案】![]()
![]()
【解析】
根据函数的奇偶性,单调性、零点和函数的图像可写出相应的函数解析式,得出答案.
由题意得:符合上述①②④条件的一个函数的解析式可以是![]() ,
,
因为![]() 的定义域为
的定义域为![]() ,其图像是一条连续不断的抛物线,所以函数满足①;
,其图像是一条连续不断的抛物线,所以函数满足①;
因为![]() ,所以函数
,所以函数![]() 是偶函数;
是偶函数;
因为当![]() 时,
时,![]() ,所以函数
,所以函数![]() 恰有两个零点:
恰有两个零点:![]() ,
,
所以函数![]() 满足条件①②④;
满足条件①②④;
符合上述①②③④条件的一个函数的解析式可以是![]() ,
,
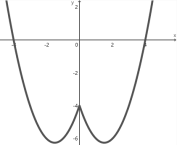
理由如下:作出函数![]() 的图象如下图所示,则函数
的图象如下图所示,则函数![]() 的图像是一条连续不断的曲线,
的图像是一条连续不断的曲线,
函数![]() 的图像关于y轴对称,所以函数
的图像关于y轴对称,所以函数![]() 是偶函数,
是偶函数,
又![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,所以函数
上单调递增,所以函数![]() 在
在![]() 上不是单调函数,
上不是单调函数,
且当![]() 时,
时,![]() ,所以函数
,所以函数![]() 恰有两个零点:
恰有两个零点:![]() .
.
所以函数![]() 满足条件①②③④.
满足条件①②③④.
故答案为:![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,三棱锥![]() 中,
中,![]() ,
,![]() 是正三角形,且平面
是正三角形,且平面![]() 平面ABC,
平面ABC,![]() ,E,G分别为AB,BC的中点.
,E,G分别为AB,BC的中点.

(Ⅰ)证明:![]() 平面ABD;
平面ABD;
(Ⅱ)若F是线段DE的中点,求AC与平面FGC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 在左、右焦点分别为
在左、右焦点分别为![]() ,
,![]() ,上顶点为点
,上顶点为点![]() ,若
,若![]() 是面积为
是面积为![]() 的等边三角形.
的等边三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,
,![]() 是椭圆
是椭圆![]() 上的两点,且
上的两点,且![]() ,求使
,求使![]() 的面积最大时直线
的面积最大时直线![]() 的方程(
的方程(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】算盘是中国传统的计算工具,其形长方,周为木框,内贯直柱,俗称“档”,档中横以梁,梁上两珠,每珠作数五,梁下五珠,每珠作数一.算珠梁上部分叫上珠,梁下部分叫下珠.例如:在十位档拨上一颗上珠和一颗下珠,个位档拨上一颗上珠,则表示数字65.若在个、十、百、千位档中随机选择一档拨一颗上珠,再随机选择两个档位各拨一颗下珠,则所拨数字大于200的概率为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )

A. 甲的极差是29 B. 甲的中位数是24
C. 甲罚球命中率比乙高 D. 乙的众数是21
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com