
【题目】已知数列{an}满足:a1=1,|an+1-an|=pn,n∈N*,Sn为数列{an}的前n项和.
(1)若{an}是递增数列,且a1,2a2,3a3成等差数列,求p的值;
(2)若p=![]() ,且{a2n-1}是递增数列,{a2n}是递减数列,求数列{an}的通项公式;
,且{a2n-1}是递增数列,{a2n}是递减数列,求数列{an}的通项公式;
(3)在(2)的条件下,令cn=n(an+1-an),求数列{cn}的前n项和Tn.
【答案】(1)p=![]() .(2)an=
.(2)an=![]() +
+![]() ·
·![]() .(3)
.(3)![]()
【解析】分析:(1)由题意得到关于p的方程,解方程可得p=![]() .
.
(2)由题意可知a2n+1-a2n-1>0,讨论可得a2n-a2n-1=![]() . 同理有a2n+1-a2n=
. 同理有a2n+1-a2n=![]() . 则数列的通项公式为an=
. 则数列的通项公式为an=![]() +
+![]() ·
·![]() .
.
(3)结合(2)中的结果首先求得数列![]() 的通项公式,然后求解其前n项和即可.
的通项公式,然后求解其前n项和即可.
详解:(1)因为{an}是递增数列,所以an+l-an=an+1-an=pn.
因为a1=1,a1,2a2,3a3成等差数列,所以4a2=a1+3a3,
则3a3-3a2=a2-a1,即3p2-p=0,解得p=![]() 或p=0.
或p=0.
当p=0时,an+1=an,这与{an}是递增数列矛盾,
所以p=![]() .
.
(2)由于{a2n-1}是递增数列,因而a2n+1-a2n-1>0,
所以(a2n+1-a2n)+(a2n-a2n-1)>0.
因为![]() <
<![]() ,所以a2n+1-a2n<a2n-a2n-1.
,所以a2n+1-a2n<a2n-a2n-1.
所以a2n-a2n-1>0,
因此a2n-a2n-1=(![]() )2n-1=
)2n-1=![]() .
.
因为{a2n}是递减数列,同理可得,a2n+1-a2n<0,
所以a2n+1-a2n=-(![]() )2n=
)2n=![]() .
.
所以an+1-an=![]() .
.
于是an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=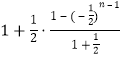 =1+
=1+![]() -
-![]() +…+
+…+![]() ,
,
所以数列{an}的通项公式为an=![]() +
+![]() ·
·![]() .
.
(3)由题意可知:![]()
![]()
![]() ,
,
则数列{cn}的前n项和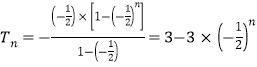 .
.


科目:高中数学 来源: 题型:
【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组: ![]()
![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图: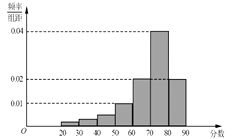
(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家举行大型的促销活动,经测算某产品当促销费用为x万元时,销售量t万件满足t=5- ![]() (其中0
(其中0 ![]() x
x ![]() a,a为正常数),现假定生产量与销售量相等,已知生产该产品t万件还需投入成本(10+2t)万元(不含促销费用),产品的销售价格定为5+
a,a为正常数),现假定生产量与销售量相等,已知生产该产品t万件还需投入成本(10+2t)万元(不含促销费用),产品的销售价格定为5+ ![]() 万元/万件.
万元/万件.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若平面点集 ![]() 满足:任意点
满足:任意点 ![]() ,存在
,存在 ![]() ,都有
,都有 ![]() ,则称该点集
,则称该点集 ![]() 是“
是“ ![]() 阶聚合”点集。现有四个命题:
阶聚合”点集。现有四个命题:
①若 ![]() ,则存在正数
,则存在正数 ![]() ,使得
,使得 ![]() 是“
是“ ![]() 阶聚合”点集;
阶聚合”点集;
②若 ![]() ,则
,则 ![]() 是“
是“ ![]() 阶聚合”点集;
阶聚合”点集;
③若 ![]() ,则
,则 ![]() 是“2阶聚合”点集;
是“2阶聚合”点集;
④若 ![]() 是“
是“ ![]() 阶聚合”点集,则
阶聚合”点集,则 ![]() 的取值范围是
的取值范围是 ![]() .
.
其中正确命题的序号为( )
A.①④
B.②③
C.①②
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)
已知正项数列![]() 满足:对任意正整数
满足:对任意正整数![]() ,都有
,都有![]() 成等差数列,
成等差数列,![]() 成等比数列,且
成等比数列,且![]()
(Ⅰ)求证:数列![]() 是等差数列;
是等差数列;
(Ⅱ)求数列![]() 的通项公式;
的通项公式;
(Ⅲ) 设![]() 如果对任意正整数
如果对任意正整数![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com