
分析 由函数y=x3-6ax+3a在(0,1)内有极小值,求导可得,导函数在(0,1)内至少有一个实数根,分a>0、a=0、a<0三种情况,求得实数a的取值范围.
解答 解:对于函数y=x3-6ax+3a,求导可得y′=3x2-6a,
∵函数y=x3-6ax+3a在(0,1)内有极小值,
∴y′=3x2-6a=0,则其有一根在(0,1)内,当a>0时,3x2-6a=0两根为±$\sqrt{2a}$,
若有一根在(0,1)内,则0<$\sqrt{2a}$<1,即0<a<$\frac{1}{2}$.
当a=0时,3x2-6a=0两根相等,均为0,f(x)在(0,1)内无极小值.
当a<0时,3x2-6a=0无根,f(x)在(0,1)内无极小值,
综合可得,0<a<$\frac{1}{2}$,
故答案为:$(0,\frac{1}{2})$.
点评 本题考查利用导数研究函数的极值问题,体现了转化的思想方法,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
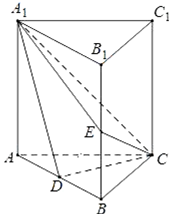 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{\sqrt{2}}{2}$AB.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=$\frac{\sqrt{2}}{2}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
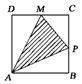 如图所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积为y的函数,则y=f(x)的图象形状大致是下列图中的( )
如图所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积为y的函数,则y=f(x)的图象形状大致是下列图中的( )| A. | 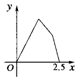 | B. | 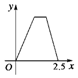 | C. | 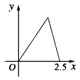 | D. | 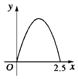 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x<0或x>2 | B. | x≥0或x≤-2 | C. | x<-1或x>4 | D. | $x≤-\frac{1}{2}$或x≥3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
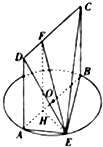 如图,AB为圆O的直径,E是圆O上不同于A,B的动点,四边形ABCD为矩形,且AB=2,AD=1,平面ABCD⊥平面ABE.
如图,AB为圆O的直径,E是圆O上不同于A,B的动点,四边形ABCD为矩形,且AB=2,AD=1,平面ABCD⊥平面ABE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com