
【题目】为了调查教师对教育改革认识水平,现从某市年龄在![]() 的教师队伍中随机选取100名教师,得到的频率分布直方图如图所示,若从年龄在
的教师队伍中随机选取100名教师,得到的频率分布直方图如图所示,若从年龄在![]() 中用分层抽样的方法选取6名教师代表.
中用分层抽样的方法选取6名教师代表.

(1)求年龄在![]() 中的教师代表人数;
中的教师代表人数;
(2)在这6名教师代表中随机选取2名教师,求在![]() 中至少有一名教师被选中的概率.
中至少有一名教师被选中的概率.
【答案】(1)2名;(2)![]()
【解析】
(1)根据分层抽样的比例关系计算得到答案.
(2)记在![]() 中选取2名教师代表为a,b,其余的4名代表为A、B、C、D,列出所有情况和满足条件的情况,相除得到答案.
中选取2名教师代表为a,b,其余的4名代表为A、B、C、D,列出所有情况和满足条件的情况,相除得到答案.
(1)由频率分布直方图得:
年龄在![]() 的教师有
的教师有![]() ,
,
年龄在![]() 的教师有
的教师有![]() ,
,
年龄在![]() 的教师有
的教师有![]() ,
,
设年龄在![]() 的教师代表人数为x,则
的教师代表人数为x,则![]() ,∴
,∴![]()
∴从年龄在![]() 中选取教师代表人数为2名;
中选取教师代表人数为2名;
(2)记在![]() 中选取2名教师代表为a,b,其余的4名代表为A、B、C、D
中选取2名教师代表为a,b,其余的4名代表为A、B、C、D
从这6名教师中选2名教师的选法为:
ab,aA,aB,aC,aD,
bA,bB,bC,bD,
AB,AC,AD,
BC,BD,
CD
以上共15种
在![]() 中至少有一名教师被选中的选法为:
中至少有一名教师被选中的选法为:
ab,aA,aB,aC,aD,
bA,bB,bC,bD
以上9种
在![]() 中至少有一名教师被选中为事件A,则
中至少有一名教师被选中为事件A,则![]() .
.
∴在[35,40)中至少有一名教师被选中的概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】f(x)是定义在D上的函数,若对任何实数α∈(0,1)以及D中的任意两数x1,x2,恒有f(αx1+(1﹣α)x2)≤αf(x1)+(1﹣α)f(x2),则称f(x)为定义在D上的C函数.
(1)试判断函数f1(x)=x2,![]() 中哪些是各自定义域上的C函数,并说明理由;
中哪些是各自定义域上的C函数,并说明理由;
(2)若f(x)是定义域为![]() 的函数且最小正周期为T,试证明f(x)不是R上的C函数.
的函数且最小正周期为T,试证明f(x)不是R上的C函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]()
(1)求圆![]() 关于直线
关于直线![]() 对称的圆
对称的圆![]() 的标准方程;
的标准方程;
(2)过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为8,求直线
截得的弦长为8,求直线![]() 的方程;
的方程;
(3)当![]() 取何值时,直线
取何值时,直线![]() 与圆
与圆![]() 相交的弦长最短,并求出最短弦长.
相交的弦长最短,并求出最短弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义域均为D的三个函数f(x),g(x),h(x)满足条件:对任意x∈D,点(x,g(x)与点(x,h(x)都关于点(x,f(x)对称,则称h(x)是g(x)关于f(x)的“对称函数”.已知g(x)=![]() ,f(x)=2x+b,h(x)是g(x)关于f(x)的“对称函数”,且h(x)≥g(x)恒成立,则实数b的取值范围是_____.
,f(x)=2x+b,h(x)是g(x)关于f(x)的“对称函数”,且h(x)≥g(x)恒成立,则实数b的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲厂以![]() 千克/小时的速度匀速生产某种产品(生产条件要求
千克/小时的速度匀速生产某种产品(生产条件要求![]() ),每小时可获得利润是
),每小时可获得利润是![]() 元.
元.
(1)要使生产该产品![]() 小时获得的利润不低于
小时获得的利润不低于![]() 元,求
元,求![]() 的取值范围;
的取值范围;
(2)要使生产![]() 千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求此最大利润.
千克该产品获得的利润最大,问:甲厂应该选取何种生产速度?并求此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知顶点![]() ,
,![]() ,动点
,动点![]() 分别在
分别在![]() 轴,
轴,![]() 轴上移动,延长
轴上移动,延长![]() 至点
至点![]() ,使得
,使得![]() ,且
,且![]() .
.
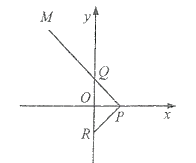
(1)求动点![]() 的轨迹
的轨迹![]() ;
;
(2)过点![]() 分别作直线
分别作直线![]() 交曲线于
交曲线于![]() 两点,若直线
两点,若直线![]() 的倾斜角互补,证明:直线的斜率为定值;
的倾斜角互补,证明:直线的斜率为定值;
(3)过点![]() 分别作直线
分别作直线![]() 交曲线于
交曲线于![]() 两点,若
两点,若![]() ,直线
,直线![]() 是否经过定点?若是,求出该定点,若不是,说明理由.
是否经过定点?若是,求出该定点,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分15分)已知中心在原点O,焦点在x轴上,离心率为![]() 的椭圆过点(
的椭圆过点(![]() ,
,![]() ).
).
(Ⅰ) 求椭圆的方程;
(Ⅱ) 设不过原点O的直线l与该椭圆交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.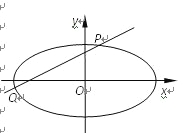
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com