练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知某二次函数的最大值为3，图象的顶点在直线y=x+1上，并且图象经过点（3，2），求二次函数的解析式．
    设二次函数解析式为y=a（x-m）2+m+1，
    二次函数的最大值为3，
    ∴m+1=3，m=2．
    ∴函数解析式为：y=a（x-2）2+3，
    又因为图象过点（3，2），
    则有2=a（3-2）2+3，
    解得：a=1
    故二次函数解析式为：y=-x2+4x-1
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    17、已知某二次函数的最大值为3，图象的顶点在直线y=x+1上，并且图象经过点（3，2），求二次函数的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

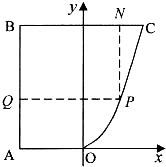    某地方政府为科技兴市，欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区，已知AB⊥BC，OA∥BC，且AB=BC=6km，AO=3km，曲线段OC是二次函数y=ax2图象的一段，如果要使矩形的相邻两边分别落在AB，BC上，且一个顶点落在曲线段OC上，问应如何规划才能使矩形工业园区BQPN的用地面积最大？并求出最大的用地面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    据市场分析，粤西某海鲜加工公司，当月产量在10吨至25吨时，月生产总成本y（万元）可以看成月产量x（吨）的二次函数．当月产量为10吨时，月总成本为20万元；当月产量为15吨时，月总成本最低为17.5万元．
    （1）写出月总成本y（万元）关于月产量x（吨）的函数关系；
    （2）已知该产品销售价为每吨1.6万元，那么月产量为多少时，可获最大利润；
    （3）当月产量为多少吨时，每吨平均成本最低，最低成本是多少万元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知某二次函数的最大值为3，图象的顶点在直线y=x+1上，并且图象经过点（3，2），求二次函数的解析式．

    查看答案和解析>>

    同步练习册答案