

 HA故四边形AEFH为平行四边形所以AE∥DF,又根据中点的性质可得FG∥SD从而将异面直线转化为了相交直线即∠HFG或其补角即为异面直线AE、SD所成的角然后再利用余弦定理求∠HFG得余弦值即可.
HA故四边形AEFH为平行四边形所以AE∥DF,又根据中点的性质可得FG∥SD从而将异面直线转化为了相交直线即∠HFG或其补角即为异面直线AE、SD所成的角然后再利用余弦定理求∠HFG得余弦值即可.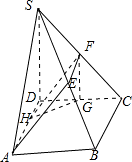
 BC,取AD的中点H连接HF则可得EF
BC,取AD的中点H连接HF则可得EF HA故四边形AEFH为平行四边形所以AE∥DF
HA故四边形AEFH为平行四边形所以AE∥DF a,FG=
a,FG= a,HG=
a,HG=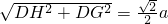
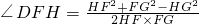 =
= >0
>0


科目:高中数学 来源: 题型:
 (文做理不做)已知:正四棱锥S-ABCD的高为
(文做理不做)已知:正四棱锥S-ABCD的高为| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com