
【题目】设![]() 是两条不同的直线,
是两条不同的直线,![]() 是三个不同的平面,给出下列四个命题:①若
是三个不同的平面,给出下列四个命题:①若![]() ,则
,则![]() ; ②若
; ②若![]() 则
则![]() ;③若
;③若![]() ,则
,则![]() ; ④若
; ④若![]() ,则
,则![]() ,其中正确命题的序号是( )
,其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 的图象经过
的图象经过![]() 和
和![]() 两点,如图所示,且函数
两点,如图所示,且函数![]() 的值域为
的值域为![]() .过该函数图象上的动点
.过该函数图象上的动点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() .
.
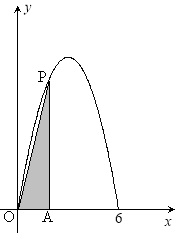
(I)求函数![]() 的解析式;
的解析式;
(Ⅱ)记![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某高中随机抽取部分高二学生,调査其到校所需的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中到校所需时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() .
.

(1)求直方图中![]() 的值;
的值;
(2)如果学生到校所需时间不少于1小时,则可申请在学校住宿.若该校录取1200名新生,请估计高二新生中有多少人可以申请住宿;
(3)以直方图中的频率作为概率,现从该学校的高二新生中任选4名学生,用![]() 表示所选4名学生中“到校所需时间少于40分钟”的人数,求
表示所选4名学生中“到校所需时间少于40分钟”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+x2+bx(a为实常数).
(1)若a=﹣2,b=﹣3,求f(x)的单调区间;
(2)若b=0,且a>﹣2e2 , 求函数f(x)在[1,e]上的最小值及相应的x值;
(3)设b=0,若存在x∈[1,e],使得f(x)≤(a+2)x成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校200名学生的数学期中考试成绩频率分布直方图如图所示,其中成绩分组区间是![]() .
.
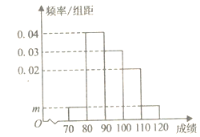
(1)求图中m的值;
(2)根据频率分布直方图,估计这200名学生的平均分(同一组中的数据用该组区间的中间值作代表)和中位数(四舍五入取整数);
(3)若这200名学生的数学成绩中,某些分数段的人数x与英语成绩相应分数段的人数y之比如下表所示,求英语成绩在![]() 的人数.
的人数.
分数段 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) |
x:y | 1:2 | 2:1 | 6:5 | 1:2 | 1:1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从高三男生中随机抽取n名学生的身高,将数据整理,得到的频率分布表如表所示:
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.05 |
第2组 |
| a | 0.35 |
第3组 |
| 30 | b |
第4组 |
| 20 | 0.20 |
第5组 |
| 10 | 0.10 |
合计 | n | 1.00 | |
(1)求出频率分布表中![]() 的值,并完成下列频率分布直方图;
的值,并完成下列频率分布直方图;
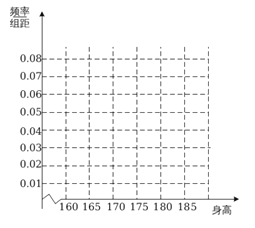
(2)为了能对学生的体能做进一步了解,该校决定在第1,4,5组中用分层抽样取7名学生进行不同项目的体能测试,若在这7名学生中随机抽取2名学生进行引体向上测试,求第4组中至少有一名学生被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数φ(x)= ![]() ,a>0
,a>0
(1)若函数f(x)=lnx+φ(x),在(1,2)上只有一个极值点,求a的取值范围;
(2)若g(x)=|lnx|+φ(x),且对任意x1 , x2∈(0,2],且x1≠x2 , 都有 ![]() <﹣1,求a的取值范围.
<﹣1,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆 ![]() +
+ ![]() =1(a>b>0)的左焦点为F,右顶点为A,离心率为
=1(a>b>0)的左焦点为F,右顶点为A,离心率为 ![]() .已知A是抛物线y2=2px(p>0)的焦点,F到抛物线的准线l的距离为
.已知A是抛物线y2=2px(p>0)的焦点,F到抛物线的准线l的距离为 ![]() .
.
(Ⅰ)求椭圆的方程和抛物线的方程;
(Ⅱ)设l上两点P,Q关于x轴对称,直线AP与椭圆相交于点B(B异于A),直线BQ与x轴相交于点D.若△APD的面积为 ![]() ,求直线AP的方程.
,求直线AP的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在ABC中,角A,B,C的对边分别为a,b,c,若△ABC为锐角三角形,且满足sinB(1+2cosC)=2sinAcosC+cosAsinC,则下列等式成立的是( )
A.a=2b
B.b=2a
C.A=2B
D.B=2A
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com