
【题目】已知函数f(x)=x|x﹣a|+2x.
(1)若函数f(x)在R上是增函数,求实数a的取值范围;
(2)求所有的实数a,使得对任意x∈[1,2]时,函数f(x)的图象恒在函数g(x)=2x+1图象的下方;
(3)若存在a∈[﹣4,4],使得关于x的方程f(x)=tf(a)有三个不相等的实数根,求实数t的取值范围.
【答案】
(1)解: ![]()
由f(x)在R上是增函数,则 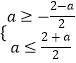 即﹣2≤a≤2,则a范围为﹣2≤a≤2;
即﹣2≤a≤2,则a范围为﹣2≤a≤2;
(2)解:由题意得对任意的实数x∈[1,2],f(x)<g(x)恒成立,
即x|x﹣a|<1,当x∈[1,2]恒成立,即 ![]() ,
, ![]() ,
, ![]() ,故只要
,故只要 ![]() 且
且 ![]() 在x∈[1,2]上恒成立即可,
在x∈[1,2]上恒成立即可,
在x∈[1,2]时,只要 ![]() 的最大值小于a且
的最大值小于a且 ![]() 的最小值大于a即可,
的最小值大于a即可,
而当x∈[1,2]时, ![]() ,
, ![]() 为增函数,
为增函数, ![]() ;
;
当x∈[1,2]时, ![]() ,
, ![]() 为增函数,
为增函数, ![]() ,
,
所以 ![]() ;
;
(3)解:当﹣2≤a≤2时,f(x)在R上是增函数,则关于x的方程f(x)=tf(a)不可能有三个不等的实数根;
则当a∈(2,4]时,由 ![]() 得x≥a时,f(x)=x2+(2﹣a)x对称轴
得x≥a时,f(x)=x2+(2﹣a)x对称轴 ![]() ,
,
则f(x)在x∈[a,+∞)为增函数,此时f(x)的值域为[f(a),+∞)=[2a,+∞),x<a时,f(x)=﹣x2+(2+a)x对称轴 ![]() ,
,
则f(x)在 ![]() 为增函数,此时f(x)的值域为
为增函数,此时f(x)的值域为 ![]() ,f(x)在
,f(x)在 ![]() 为减函数,此时f(x)的值域为
为减函数,此时f(x)的值域为 ![]() ;
;
由存在a∈(2,4],方程f(x)=tf(a)=2ta有三个不相等的实根,则 ![]() ,
,
即存在a∈(2,4],使得 ![]() 即可,令
即可,令 ![]() ,
,
只要使t<(g(a))max即可,而g(a)在a∈(2,4]上是增函数, ![]() ,
,
故实数t的取值范围为 ![]() ;(15分)
;(15分)
同理可求当a∈[﹣4,﹣2)时,t的取值范围为 ![]() ;
;
综上所述,实数t的取值范围为 ![]() .
.
【解析】(1)由题意知f(x)在R上是增函数,则 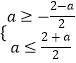 即﹣2≤a≤2,则a范围.(2)由题意得对任意的实数x∈[1,2],f(x)<g(x)恒成立,即
即﹣2≤a≤2,则a范围.(2)由题意得对任意的实数x∈[1,2],f(x)<g(x)恒成立,即 ![]() ,
, ![]() ,
, ![]() ,故只要
,故只要 ![]() 且
且 ![]() 在x∈[1,2]上恒成立即可,在x∈[1,2]时,只要
在x∈[1,2]上恒成立即可,在x∈[1,2]时,只要 ![]() 的最大值小于a且
的最大值小于a且 ![]() 的最小值大于a即可.由此可知答案.(3)当﹣2≤a≤2时,f(x)在R上是增函数,则关于x的方程f(x)=tf(a)不可能有三个不等的实数根存在a∈(2,4],方程f(x)=tf(a)=2ta有三个不相等的实根,则
的最小值大于a即可.由此可知答案.(3)当﹣2≤a≤2时,f(x)在R上是增函数,则关于x的方程f(x)=tf(a)不可能有三个不等的实数根存在a∈(2,4],方程f(x)=tf(a)=2ta有三个不相等的实根,则 ![]() ,即存在a∈(2,4],使得
,即存在a∈(2,4],使得 ![]() 即可,由此可证出实数t的取值范围为
即可,由此可证出实数t的取值范围为 ![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是等比数列,且b2=3,b3=9,a1=b1 , a14=b4 . (Ⅰ)求{an}的通项公式;
(Ⅱ)设cn=an+bn , 求数列{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为1,圆心角为 ![]() 的圆弧
的圆弧 ![]() 上有一点C.
上有一点C. 
(1)若C为圆弧AB的中点,点D在线段OA上运动,求| ![]() +
+ ![]() |的最小值;
|的最小值;
(2)若D,E分别为线段OA,OB的中点,当C在圆弧 ![]() 上运动时,求
上运动时,求 ![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,g(x)=1-ax2.
,g(x)=1-ax2.
(1)若函数f(x)和g(x)的图象在x=1处的切线平行,求a的值;
(2)当x∈[0,1]时,不等式f(x)≤g(x)恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察以下三个等式: sin215°﹣sin245°+sin15°cos45°=﹣ ![]() ,
,
sin220°﹣sin250°+sin20°cos50°=﹣ ![]() ,
,
sin230°﹣sin260°+sin30°cos60°=﹣ ![]() ;
;
猜想出一个反映一般规律的等式: .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2ax﹣ ![]() +lnx在x=1与x=
+lnx在x=1与x= ![]() 处都取得极值. (Ⅰ) 求a,b的值;
处都取得极值. (Ⅰ) 求a,b的值;
(Ⅱ)设函数g(x)=x2﹣2mx+m,若对任意的x1∈[ ![]() ,2],总存在x2∈[
,2],总存在x2∈[ ![]() ,2],使得g(x1)≥f(x2)﹣lnx2 , 求实数m的取值范围.
,2],使得g(x1)≥f(x2)﹣lnx2 , 求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)对任意的x∈(﹣ ![]() ,
, ![]() )满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是( )
)满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是( )
A.![]() f(﹣
f(﹣ ![]() )<f(﹣
)<f(﹣ ![]() )
)
B.![]() f(
f( ![]() )<f(
)<f( ![]() )??
)??
C.f(0)>2f( ![]() )
)
D.f(0)> ![]() f(
f( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在[﹣1,1]的函数f(x)满足下列两个条件:①任意的x∈[﹣1,1],都有f(﹣x)=﹣f(x);②任意的m,n∈[0,1],当m≠n,都有 ![]() <0,则不等式f(1﹣3x)<f(x﹣1)的解集是( )
<0,则不等式f(1﹣3x)<f(x﹣1)的解集是( )
A.[0, ![]() )
)
B.( ![]() ,
, ![]() ]
]
C.[﹣1, ![]() )
)
D.[ ![]() ,1]
,1]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com