
【题目】已知函数f(x)=xln x-aex(e为自然对数的底数)有两个极值点,则实数a的取值范围是( )
A.![]() B.(0,e)
B.(0,e)
C.![]() D.(-∞,e)
D.(-∞,e)
【答案】A
【解析】
先求函数导数,再根据题意将导函数为零转化为两个函数![]() 有两个不同的交点,然后求
有两个不同的交点,然后求![]() 的导函数零点,列表分析导函数符号变化规律,确定单调性,进而确定
的导函数零点,列表分析导函数符号变化规律,确定单调性,进而确定![]() 图象,最后根据图象确定实数a的取值范围.
图象,最后根据图象确定实数a的取值范围.
f(x)=x ln x-aex(x>0),∴f′(x)=ln x+1-aex(x>0),由已知函数f(x)有两个极值点可得y=a和g(x)=![]() 在(0,+∞)上有两个交点,
在(0,+∞)上有两个交点,
g′(x)=![]() (x>0),令h(x)=
(x>0),令h(x)=![]() -ln x-1,
-ln x-1,
则h′(x)=-![]() -
-![]() <0,
<0,
∴h(x)在(0,+∞)上单调递减且h(1)=0,
∴当x∈(0,1]时,h(x)≥0,即g′(x)≥0,g(x)在(0,1]上单调递增,g(x)≤g(1)=![]() ,
,
当x∈(1,+∞)时,h(x)<0,即g′(x)<0,g(x)在(1,+∞)上单调递减,
故g(x)max=g(1)=![]() ,
,
而x→0时,g(x)→-∞,x→+∞时,g(x)→0;
若y=a和g(x)在(0,+∞)上有两个交点,只需0<a<![]() .
.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,
,![]() ,
,![]() ,E为PD的中点,点F在PC上,且
,E为PD的中点,点F在PC上,且![]() .
.
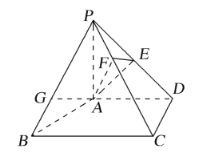
(1)求证:平面![]() 平面PAD;
平面PAD;
(2)求二面角F-AE-P的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 为一张台球桌面,
为一张台球桌面,![]() ,
,![]() .从点
.从点![]() 击出一个球,其可无限次经台球桌四边反弹运行.已知该球经过矩形
击出一个球,其可无限次经台球桌四边反弹运行.已知该球经过矩形![]() 的中心
的中心![]() .
.
(1)试求所有整点![]()
![]() 的个数,使得该球可以经过点
的个数,使得该球可以经过点![]() ;
;
(2)若该球在上述![]() 、
、![]() 两点间的最短路径长为
两点间的最短路径长为![]() ,求
,求![]() 的最大值.
的最大值.
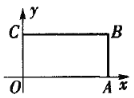
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年3月21日是世界睡眠日,良好的睡眠状况是保持身体健康的重要基础.为了做好今年的世界睡眠日宣传工作,某社区从本辖区内同一年龄层次的人员中抽取了100人,通过问询的方式得到他们在一周内的睡眠时间(单位:小时),并绘制出如右的频率分布直方图:
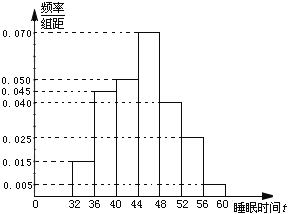
(Ⅰ)求这100人睡眠时间的平均数![]() (同一组数据用该组区间的中点值代替,结果精确到个位);
(同一组数据用该组区间的中点值代替,结果精确到个位);
(Ⅱ)由直方图可以认为,人的睡眠时间![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() 近似地等于样本平均数
近似地等于样本平均数![]() ,
,![]() 近似地等于样本方差
近似地等于样本方差![]() ,
,![]() .假设该辖区内这一年龄层次共有10000人,试估计该人群中一周睡眠时间位于区间(39.2,50.8)的人数.
.假设该辖区内这一年龄层次共有10000人,试估计该人群中一周睡眠时间位于区间(39.2,50.8)的人数.
附:![]() .若随机变量
.若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]()
![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,过
,过![]() 的直线交椭圆于
的直线交椭圆于![]() ,
,![]() 两点,若椭圆
两点,若椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 的周长为
的周长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设不经过椭圆的中心而平行于弦![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,
,![]() ,设弦
,设弦![]() ,
,![]() 的中点分别为
的中点分别为![]() ,证明:
,证明:![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对由![]() 个
个![]() 、
、![]() 个
个![]() 和
和![]() 个
个![]() 排成的行,在其下面重新定义一行(比上面一行少一个字母).若其头上的两个字母不同,则在该位置写上第三个字母;若其头上的两个字母相同,则在该位置写上该字母.对新得到的行重复上面的操作,直到变为一个字母为止.图给出了
排成的行,在其下面重新定义一行(比上面一行少一个字母).若其头上的两个字母不同,则在该位置写上第三个字母;若其头上的两个字母相同,则在该位置写上该字母.对新得到的行重复上面的操作,直到变为一个字母为止.图给出了![]() 的一个例子.
的一个例子.

求所有的正整数![]() ,使得对任意的初始排列,经上述操作后,所得到的三角形的三个顶点上的字母要么全相同,要么两两不同.
,使得对任意的初始排列,经上述操作后,所得到的三角形的三个顶点上的字母要么全相同,要么两两不同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com