ЃЈЂёЃЉвРЬтвтга
|A1B2|==Ёрa
2+b
2=7ЁЃЈ1ЗжЃЉ
гжгЩS
ЁѕA
1B
1A
2B
2=2S
ЁѕB
1F
1B
2F
2ЃЎга2a•b=2•2c•bЃЌЁрa=2cЁЃЈ2ЗжЃЉ
НтЕУa
2=4ЃЌb
2=3ЃЌЁЃЈ3ЗжЃЉЃЌ
ЙЪЭждВCЕФЗНГЬЮЊ
+=1ЃЎЁЃЈ4ЗжЃЉ
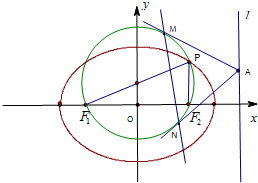
ЃЈЂђЃЉЕБжБЯпmЕФаБТЪДцдкЪБЃЌЩшжБЯпmЕФЗНГЬЮЊy=kЃЈx-1ЃЉ+1ЃЌMЃЈx
1ЃЌy
1ЃЉЃЌNЃЈx
2ЃЌy
2ЃЉЃЌ
дђ
+=1ЃЌ
+=1ЃЌ
СНЪНЯрМѕЕУЃК
k==-ЁСЃЎ
ЁпQЪЧMNЕФжаЕуЃЌ
ЁрПЩЕУжБЯпmЕФаБТЪЮЊ
k==-ЃЌЃЈ7ЗжЃЉ
ЕБжБЯпmЕФаБТЪВЛДцдкЪБЃЌНЋx=1ДњШыЭждВЗНГЬВЂНтЕУ
M(1ЃЌ)ЃЌ
N(1ЃЌ-)ЃЌ
етЪБMNЕФжаЕуЮЊЃЈ1ЃЌ0ЃЉЃЌ
Ёрx=1ВЛЗћКЯЬтЩшвЊЧѓЃЎЁЃЈ8ЗжЃЉ
злЩЯЃЌжБЯпmЕФЗНГЬЮЊ3x+4y-7=0ЁЃЈ9ЗжЃЉ
ЃЈЂѓЃЉЩшAЃЌBСНЕуЕФзјБъЗжБ№ЮЊЃЈx
1ЃЌy
1ЃЉЃЌЃЈx
2ЃЌy
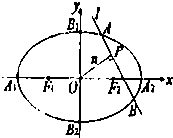
2ЃЉЃЌМйЩшТњзуЬтЩшЕФжБЯпlДцдкЃЌ
ЃЈiЃЉЕБlВЛДЙжБгкxжсЪБЃЌЩшlЕФЗНГЬЮЊy=kx+mЃЌгЩlгыnДЙжБЯрНЛгкPЕуЧв
||=1ЕУ
=1ЃЌМДm
2=k
2+1ЃЌЁЃЈ10ЗжЃЉ
гжЁпвдABЮЊжБОЖЕФдВЙ§дЕуЃЌЁрOAЁЭOBЃЌЁрx
1x
2+y
1y
2=0ЃЎ
НЋy=kx+mДњШыЭждВЗНГЬЃЌЕУЃЈ3+4k
2ЃЉx
2+8kmx+ЃЈ4m
2-12ЃЉ=0ЃЌ
гЩЧѓИљЙЋЪНПЩЕУ
x1+x2=ЃЌЂм
x1x2=ЃЎЂн
0=x
1x
2+y
1y
2=x
1x
2+ЃЈkx
1+mЃЉЃЈkx
2+mЃЉ=
x1x2+k2x1x2+km(x1+x2)+m2=
(1+k2)x1x2+km(x1+x2)+m2ЃЌ
НЋЂмЃЌЂнДњШыЩЯЪНВЂЛЏМђЕУЃЈ1+k
2ЃЉЃЈ4m
2-12ЃЉ-8k
2m
2+m
2ЃЈ3+4k
2ЃЉ=0ЃЌЂо
НЋm
2=1+k
2ДњШыЂоВЂЛЏМђЕУ-5ЃЈk
2+1ЃЉ=0ЃЌУЌЖмЃЎ
МДДЫЪБжБЯпlВЛДцдкЃЎЁЃЈ12ЗжЃЉ
ЃЈiiЃЉЕБlДЙжБгкxжсЪБЃЌТњзу
||=1ЕФжБЯпlЕФЗНГЬЮЊx=1Лђx=-1ЃЌ
гЩAЁЂBСНЕуЕФзјБъЮЊЃЈ1ЃЌ
ЃЉЃЌЃЈ1ЃЌ-
ЃЉЛђЃЈ-1ЃЌ
ЃЉЃЌЃЈ-1ЃЌ-
ЃЉЃЎ
ЕБx=1ЪБЃЌ
•=ЃЈ1ЃЌ
ЃЉ•ЃЈ1ЃЌ-
ЃЉ=-
Ёй0ЃЌ
ЕБx=-1ЪБЃЌ
•=ЃЈ-1ЃЌ
ЃЉ•ЃЈ-1ЃЌ-
ЃЉ=-
Ёй0ЃЎ
ЁрДЫЪБжБЯпlвВВЛДцдкЃЎ
злЩЯЫљЪіЃЌЪЙ
•=0ГЩСЂЕФжБЯпlВЛГЩСЂЃЌМДВЛДцдкжБЯпlЪЙвдABЮЊжБОЖЕФдВЙ§дЕуЃЎ



 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ