Question

16．已知函数f（x）=$\left\{\begin{array}{l}{{a}^{x}+1，x≤0}\\{|lnx|，x＞0}\end{array}\right.$当1＜a＜2时，关于x的方程f[f（x）]=a实数解的个数为（　　）

• A． 2
• B． 3
• C． 4
• D． 5

Answer 1

分析 判断f（x）的单调性，做出f（x）的草图，得出f（t）=a的根的情况，再根据方程f（x）=t的根个数，得出结论．

解答 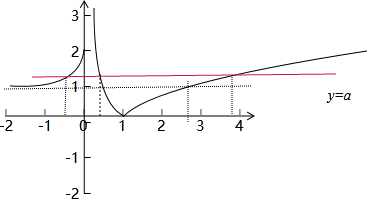解：函数f（x）=$\left\{\begin{array}{l}{{a}^{x}+1，x≤0}\\{|lnx|，x＞0}\end{array}\right.$的图象如下，令f（t）=a，
∵1＜a＜2，如图所示得，方程f（t）=a有三个根：t₁，t₂，t₃．
且t₁＜0，${t}_{2}∈（{e}^{-2}，{e}^{-1}）$，${t}_{3}∈（e，{e}^{2}）$．
方程f（x）=t₁无解，方程f（x）=t₂有两个解，方程f（x）=t₃无解．
故关于x的方程f[f（x）]=a实数解的个数为2，
故选：A．

点评 本题考查了复合函数根的存在性判断，数形结合思想，属于中档题