练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．执行如图的程序框图，则输出的n为13．

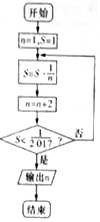
    分析 算法的功能是求满足S=1×$\frac{1}{3}$×$\frac{1}{5}$×…$\frac{1}{n}$＜$\frac{1}{2017}$的最大的正整数n+2的值，验证S=1•3•…•13＞2017，从而确定输出的n值．

    解答 解：由程序框图知：算法的功能是求满足S=1×$\frac{1}{3}$×$\frac{1}{5}$×…$\frac{1}{n}$＜$\frac{1}{2017}$的最大的正整数n+2的值，
    ∵S=1×3×…×13＞2017，
    ∴输出n=13．
    故答案为：13．

    点评 本题考查了直到型循环结构的程序框图，关键框图的流程判断算法的功能是解答本题的关键，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．已知两圆的方程分别为x2+y2+6x-4=0和x2+y2+6y-28=0且交于A，B两点
    （1）求AB所在的直线方程
    （2）求两圆公共弦AB的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．设公比大于零的等比数列{an}的前n项和为Sn，且a1=1，S4=5S2，数列{an}的通项公式（　　）
    A．an=2n-1B．an=3nC．2D．an=5n

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．在复平面内，若z=m2（1+i）-m（4+i）-6i，求实数m的取为何值时，复数z 是：
    （1）虚数
    （2）对应的点在第一象限．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1，（a＞0，b＞0）的两个焦点为F1、F2，点A在双曲线第一象限的图象上，△AF1F2的面积为1，且sin∠A F1F2=$\frac{1}{\sqrt{5}}$，cos∠F1AF2=$\frac{4}{5}$
    （1）求双曲线的方程
    （2）已知直线y=kx+1与双曲线相交于不同两点，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知函数f（x）（x∈R）的图象上任一点（x0，y0）处的切线方程为y-y0=（x0-2）（x02-1）（x-x0），那么函数f（x）的单调递减区间是（　　）
    A．[-1，+∞）B．（-∞，2]C．（-∞，-1）和（1，2）D．[2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知集合$A=\left\{{x|lnx≤0}\right\}，B=\left\{{x∈R|x≥\frac{1}{2}}\right\}$，则A∩B=（　　）
    A．$（{-∞，-\frac{1}{2}}）∪[{\frac{1}{2}，1}]$B．$[{\frac{1}{2}，1}]$C．（0，1]D．[1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

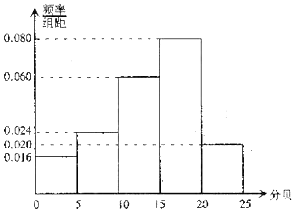    7．人耳的听力情况可以用电子测听器检测，正常人听力的等级为0-25db（分贝），并规定测试值在区间（0，5]为非常优秀，测试值在区间（5，10]为优秀，某班50名同学都进行了听力测试，所得测试值制成频率分布直方图：
    （Ⅰ）现从听力等级为（0，10]的同学中任意抽取出4人，记听力非常优秀的同学人数X，求X的分布列与数学期望．
    （Ⅱ）在（Ⅰ）中抽出的4人中任选一人参加一个更高级别的听力测试，测试规则如下：四个音叉的发声情况不同，由强到弱的次序分别为1，2，3，4，测试前将音叉随机排列，被测试的同学依次听完后给四个音叉按发音的强弱标出一组序号a1，a2，a3，a4（其中a1，a2，a3，a4为1，2，3，4的一个排列），若Y为两次排序偏离程度的一种描述，Y=|1-a1|+|2-a2|+|3-a3|+|4-a4|，求Y≤2的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．函数$f（x）={sin^2}x+\sqrt{3}sinxcosx$在区间$[{\frac{π}{4}，\frac{π}{2}}]$上的最小值为（　　）
    A．1B．$\frac{{1+\sqrt{3}}}{2}$C．$\frac{3}{2}$D．$1+\sqrt{3}$

    查看答案和解析>>

    同步练习册答案