
【题目】已知a,b是正实数,设函数f(x)=xlnx,g(x)=﹣a+xlnb.
(Ⅰ)设h(x)=f(x)﹣g(x),求h(x)的单调区间;
(Ⅱ)若存在x0 , 使x0∈[ ![]() ,
, ![]() ]且f(x0)≤g(x0)成立,求
]且f(x0)≤g(x0)成立,求 ![]() 的取值范围.
的取值范围.
【答案】解:(1)∵h(x)=f(x)﹣g(x)=xlnx+a﹣xlnb
∴h′(x)=lnx+1﹣lnb
由h′(x)>0得x> ![]() ,
,
∴h(x)在(0, ![]() )上单调递减,(
)上单调递减,( ![]() ,+∞)上单调递增.
,+∞)上单调递增.
2)由 ![]() <
< ![]() 得
得 ![]() <7
<7
(i)当 ![]() ≤
≤ ![]() ≤
≤ ![]() ,即
,即 ![]() ≤
≤ ![]() ≤
≤ ![]() 时,
时,
h(x)min=h( ![]() )=﹣
)=﹣ ![]() +a
+a
由﹣ ![]() +a≤0得
+a≤0得 ![]() ≥e,
≥e,
∴e≤ ![]() ≤
≤ ![]()
(ii)当 ![]() <
< ![]() 时,a>
时,a> ![]()
∴h(x)在[ ![]() ,
, ![]() ]上单调递增.
]上单调递增.
h(x)min=h( ![]() )=
)= ![]() (ln
(ln ![]() ﹣lnb)+a≥
﹣lnb)+a≥ ![]() (ln
(ln ![]() ﹣lnb)+a=
﹣lnb)+a= ![]() >
> 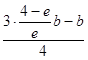 =
= ![]() b>0
b>0
∴不成立
(iii)当 ![]() >
> ![]() ,即
,即 ![]() >
> ![]() 时,a<
时,a< ![]() b
b
h(x)在[ ![]() ,
, ![]() ]上单调递减.
]上单调递减.
h(x)min=h( ![]() )=
)= ![]() (ln
(ln ![]() ﹣lnb)+a<
﹣lnb)+a< ![]() (ln
(ln ![]() lnb)+a=
lnb)+a= ![]() <
< 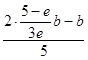 =
= ![]() <0
<0
∴当 ![]() >
> ![]() 时恒成立
时恒成立
综上所述,e≤ ![]() <7
<7
【解析】(I)根据已知求出h(x)=f(x)﹣g(x)的解析式,求出其导函数,分别求出导函数为正,为负时x的取值范围,进而可得h(x)的单调区间;(Ⅱ)根据区间的定义可得 ![]() <
< ![]() ,由f(x0)≤g(x0),结合(I)中函数的单调性,分类讨论,最后综合讨论结果,可得
,由f(x0)≤g(x0),结合(I)中函数的单调性,分类讨论,最后综合讨论结果,可得 ![]() 的取值范围.
的取值范围.
【考点精析】利用利用导数研究函数的单调性对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
极坐标系中, ![]() 为极点,半径为2的圆
为极点,半径为2的圆![]() 的圆心坐标为
的圆心坐标为![]() .
.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设直角坐标系的原点与极点![]() 重合,
重合, ![]() 轴非负关轴与极轴重合,直线
轴非负关轴与极轴重合,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),由直线
为参数),由直线![]() 上的点向圆
上的点向圆![]() 引切线,求切线长的最小值.
引切线,求切线长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果函数f(x)在[a,b]上存在x1 , x2(a<x1<x2<b)满足 ![]() ,
, ![]() ,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上的“双中值函数”,则实数a的取值范围是( )
,则称函数f(x)是[a,b]上的“双中值函数”.已知函数f(x)=x3﹣x2+a是[0,a]上的“双中值函数”,则实数a的取值范围是( )
A.![]()
B.( ![]() )
)
C.( ![]() ,1)
,1)
D.( ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分16分)如图,有一个长方形地块ABCD,边AB为2km, AD为4 km.,地块的一角是湿地(图中阴影部分),其边缘线AC是以直线AD为对称轴,以A为顶点的抛物线的一部分.现要铺设一条过边缘线AC上一点P的直线型隔离带EF,E,F分别在边AB,BC上(隔离带不能穿越湿地,且占地面积忽略不计).设点P到边AD的距离为t(单位:km),△BEF的面积为S(单位: ![]() ).
).

(1)求S关于t的函数解析式,并指出该函数的定义域;
(2)是否存在点P,使隔离出的△BEF面积S超过3 ![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥S﹣ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论中恒成立的个数为( )
(1)EP⊥AC;
(2)EP∥BD;
(3)EP∥面SBD;
(4)EP⊥面SAC.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的圆心是直线x﹣y+1=0与x轴的交点,且圆C与(x﹣2)2+(y﹣4)2=9相外切,若过点P(﹣1,1)的直线l与圆C交于A,B两点,当∠ACB最小时,弦AB的长为( )
A.4
B.![]()
C.2
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,A1B1=A1C1 , D,E分别是棱BC,CC1上的点(点D 不同于点C),且AD⊥DE,F为B1C1的中点.求证: 
(1)平面ADE⊥平面BCC1B1;
(2)直线A1F∥平面ADE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分别根据下列条件,求圆的方程:
(1)过两点(0,4),(4,6),且圆心在直线x﹣2y﹣2=0上;
(2)半径为 ![]() ,且与直线2x+3y﹣10=0切于点(2,2).
,且与直线2x+3y﹣10=0切于点(2,2).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com