
| 答对题目个数 | 0 | 1 | 2 | 3 |
| 人数 | 5 | 10 | 20 | 15 |
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:不详 题型:解答题
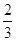 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 为取得红球的个数.
为取得红球的个数.  的分布列;
的分布列; 的数学期望
的数学期望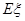 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [160,165) | 5 | 0.05 |
| 第二组 | [165,170) | 35 | 0.35 |
| 第三组 | [170,175) | 30 | a |
| 第四组 | [175,180) | b | 0.2 |
| 第五组 | [180,185) | 10 | 0.1 |
 的值;
的值;  ,求
,求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.Y的取值为0,1,2,3 |
| B.P(Y=0)+P(Y=1)+P(Y=2)+P(Y=3)=1 |
| C.若每录取1人学校奖励300元给班主任,没有录取不奖励,则班主任得奖金数为300Y |
| D.若每不录取1人学校就扣班主任300元,录取不奖励,则班主任得奖金数为-300Y |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
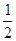 ,乙投篮一次命中的概率为
,乙投篮一次命中的概率为 .每人各投4个球,两人投篮命中的概率互不影响.
.每人各投4个球,两人投篮命中的概率互不影响.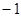 分,求乙所得分数
分,求乙所得分数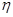 的概率分布和数学期望.
的概率分布和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 且各轮问题能否正确回答互不影响.
且各轮问题能否正确回答互不影响. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com