
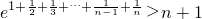 (n∈N*);
(n∈N*);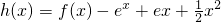 ,g(x)=elnx,h(x)与g(x)是否存在“分界线”?若存在,求出k,b的值;若不存在,请说明理由.
,g(x)=elnx,h(x)与g(x)是否存在“分界线”?若存在,求出k,b的值;若不存在,请说明理由. 得ex-1≥x,
得ex-1≥x,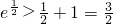 ,
,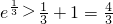 ,
,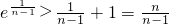 ,
,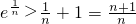 .
.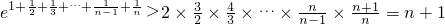 .…(9分)
.…(9分)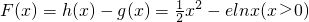 .
.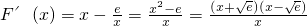 .
.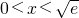 时,F'(x)<0;
时,F'(x)<0;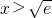 时,F'(x)>0.
时,F'(x)>0. 时F(x)取得最小值0,
时F(x)取得最小值0, 处有公共点
处有公共点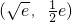 .
.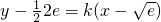 .
.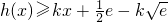 在x∈R恒成立,
在x∈R恒成立,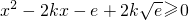 在x∈R恒成立.
在x∈R恒成立.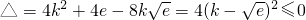 成立.
成立.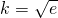 .
.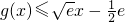 (x>0)成立.
(x>0)成立.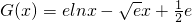 ,
,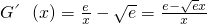 .
.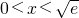 时,G'(x)>0;
时,G'(x)>0;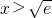 时,G'(x)<0.
时,G'(x)<0. 时G(x)取得最大值0,
时G(x)取得最大值0,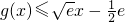 (x>0)成立.
(x>0)成立.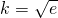 ,
,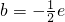 .…(14分)
.…(14分) 得ex-1≥x,把x换成t+1得et≥t+1,当且仅当t=0时等号成立.由此能够证明
得ex-1≥x,把x换成t+1得et≥t+1,当且仅当t=0时等号成立.由此能够证明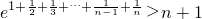 (n∈N*).
(n∈N*).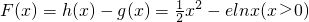 .则
.则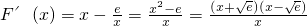 .所以当
.所以当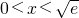 时,F'(x)<0;当
时,F'(x)<0;当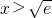 时,F'(x)>0.因此
时,F'(x)>0.因此 时F(x)取得最小值0,则h(x)与g(x)的图象在
时F(x)取得最小值0,则h(x)与g(x)的图象在 处有公共点
处有公共点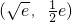 .由此能够导出
.由此能够导出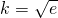 ,
,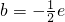 .
.

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com