分析:(1)先设出点P的坐标,利用题中条件把点M的坐标用点P的坐标表示出来,最后利用点P在圆x
2+y
2=1上即可求曲线C的方程;
(2)先把直线方程与曲线方程联立求出A、B两点的坐标之间的关系,代入
•
=0的等价结论x
1x
2+y
1y
2=0即可求λ的取值范围.
解答:解:(1)设点P的坐标为(x
0,y
0),点M的坐标为(x,y),则点Q的坐标为(0,y
0).
由
=λ,得x=λx
0,y=y
0?
x0=,y
0=y.(3分)
因为点P在圆x
2+y
2=1上,则x
02+y
02=1,所以
+y2=1(λ≠0).
故点M的轨迹C的方程为
+y2=1(λ≠0).(7分)
(2)因为直线l的斜率为0时,
•
=0,故可设直线l的方程为
x=my+.
由
得
(m2+λ2)y2+my+-λ2=0(*)(10分)
设点A(x
1,y
1),B(x
2,y
2),则
y1+y2=-,y1y2=.
因为
•
=0,则x
1x
2+y
1y
2=0,又
x1x2=m2y1 y2 +(y1+y2) +,
所以
(m2+1)(-λ2)-+(m2+λ2)=0,(13分)
因为λ≠0,所以m
2=
,由
≥0?-
≤λ≤且λ≠0.,
此时(*)的判别式△>0成立,故λ的取值范围是
[-,0)∪(0,].(15分)
点评:本题主要考查轨迹方程的求法,直线的方程,向量共线以及向量垂直等基础知识,考查用代数方法研究圆锥曲线的性质和数形结合的数学思想,考查解决问题的能力和运算能力.



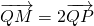 的点M的轨迹为曲线C.
的点M的轨迹为曲线C. 的点M的轨迹为曲线C.
的点M的轨迹为曲线C.