
【题目】已知数列{an}中,a1=5,a2=2,an=2an﹣1+3an﹣2 , (n≥3) (Ⅰ)证明数列{an﹣3an﹣1}成等比数列,并求数{an}列的通项公式an;
(Ⅱ)若数列bn= ![]() (an+1+an),求数列{bn}的前n项和Sn .
(an+1+an),求数列{bn}的前n项和Sn .
【答案】解:(Ⅰ)∵an=2an﹣1+3an﹣2(n≥3), ∴an+an﹣1=3(an﹣1+an﹣2),
又∵a2+a1=2+5=7,
∴数列{an+1+an}是以7为首项、3为公比的等比数列,
∴an+1+an=73n﹣1;
∵an=2an﹣1+3an﹣2(n≥3),
∴an﹣3an﹣1=﹣(an﹣1﹣3an﹣2),
又∵a2﹣3a1=2﹣35=﹣13,
∴数列{an+1﹣3an}是以﹣13为首项、﹣1为公比的等比数列,
∴an+1﹣3an=﹣13(﹣1)n﹣1;
∴an= ![]() ×(﹣1)n﹣1+
×(﹣1)n﹣1+ ![]() ×3n﹣1 .
×3n﹣1 .
(Ⅱ)由(Ⅰ),得an+1+an=73n﹣1 ,
∴bn= ![]() (an+1+an)=(2n﹣1)×3n﹣1 ,
(an+1+an)=(2n﹣1)×3n﹣1 ,
∴Sn=1×30+3×31+5×32+…+(2n﹣1)×3n﹣1 ,
∴3Sn=1×31+3×32+5×33+…+(2n﹣3)×3n﹣1+(2n﹣1)×3n ,
∴﹣2Sn=1+2(31+32+33+…+3n﹣1)﹣(2n﹣1)×3n=1+2× ![]() ﹣(2n﹣1)×3n=﹣2﹣(2n﹣2)3n ,
﹣(2n﹣1)×3n=﹣2﹣(2n﹣2)3n ,
∴Sn=(n﹣1)3n+1
【解析】(Ⅰ)通过an=2an﹣1+3an﹣2(n≥3)变形为an+λan﹣1=m(an﹣1+λan﹣2)形式计算可求.(Ⅱ)bn= ![]() (an+1+an)=(2n﹣1)×3n﹣1 , 再利用错位相减法即可求出数列{bn}的前n项和Sn .
(an+1+an)=(2n﹣1)×3n﹣1 , 再利用错位相减法即可求出数列{bn}的前n项和Sn .
【考点精析】根据题目的已知条件,利用数列的前n项和和数列的通项公式的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系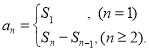 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


科目:高中数学 来源: 题型:
【题目】若函数f(x)=3sin(2x﹣ ![]() )的图象为C,则下列结论中正确的序号是 . ①图象C关于直线x=
)的图象为C,则下列结论中正确的序号是 . ①图象C关于直线x= ![]() 对称;
对称;
②图象C关于点( ![]() ,0)对称;
,0)对称;
③函数f(x)在区间(﹣ ![]() ,
, ![]() )内不是单调的函数;
)内不是单调的函数;
④由y=3sin2x的图象向右平移 ![]() 个单位长度可以得到图象C.
个单位长度可以得到图象C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)已知圆C的圆心是x﹣y+1=0与x轴的交点,且与直线x+y+3=0相切,求圆C的标准方程;
(2)若点P(x,y)在圆x2+y2﹣4y+3=0上,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际油价在某一时间内呈现出正弦波动规律:P=Asin(ωπt+ ![]() )+60(美元)[t(天),A>0,ω>0],现采集到下列信息:最高油价80美元,当t=150(天)时达到最低油价,则ω= .
)+60(美元)[t(天),A>0,ω>0],现采集到下列信息:最高油价80美元,当t=150(天)时达到最低油价,则ω= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一房产商竞标得一块扇形OPQ地皮,其圆心角∠POQ= ![]() ,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议.
,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a2=2,前n项和为 ![]() . (I)证明数列{an+1﹣an}是等差数列,并求出数列{an}的通项公式;
. (I)证明数列{an+1﹣an}是等差数列,并求出数列{an}的通项公式;
(II)设 ![]() ,数列{bn}的前n项和为Tn , 求使不等式
,数列{bn}的前n项和为Tn , 求使不等式 ![]() 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三条不重合的直线 ![]() 和两个不重合的平面
和两个不重合的平面 ![]() ,下列命题正确的是( )
,下列命题正确的是( )
A.若 ![]() ,
, ![]() ,则
,则 ![]()
B.若 ![]() ,
, ![]() ,且
,且 ![]() ,则
,则 ![]()
C.若 ![]() ,
, ![]() ,则
,则 ![]()
D.若 ![]() ,
, ![]() ,且
,且 ![]() ,则
,则 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式x2﹣ax﹣2>0的解集为{x|x<﹣1或x>b}(b>﹣1).
(1)求a,b的值;
(2)当m>﹣ ![]() 时,解关于x的不等式(mx+a)(x﹣b)>0.
时,解关于x的不等式(mx+a)(x﹣b)>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com