
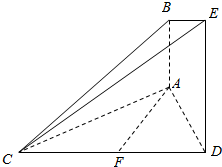
 如图所示,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2a,F为CD的中点.
如图所示,已知AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2a,F为CD的中点.分析 (1)可取CE中点为M,并连接BM,FM,从而可得到MF∥DE,MF=$\frac{1}{2}DE$,进一步便可得到MF∥AB,且MF=AB,从而四边形ABMF为平行四边形,从而有AF∥BM,这样根据线面平行的判定定理便可得到AF∥平面BCE;
(2)容易看出BM⊥平面CDE,从而可判断平面BCE⊥平面CDE,可根据线面垂直的性质及判定定理证明AF⊥平面CDE,从而有BM⊥平面CDE,这样由面面垂直的判定定理即可得到平面BCE⊥平面CDE.
解答 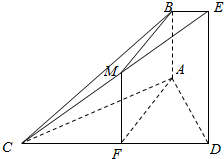 解:(1)证明:如图,取CE中点M,连接BM,FM;
解:(1)证明:如图,取CE中点M,连接BM,FM;
∵F为CD的中点;
∴MF∥DE,且$MF=\frac{1}{2}DE$;
又DE⊥平面ACD,AB⊥平面ACD,DE=2AB;
∴MF⊥平面ACD,MF∥AB,且MF=AB;
∴四边形ABMF为平行四边形;
∴AF∥BM,BM?平面BCE,AF?平面BCE;
∴AF∥平面BCE;
(2)可看出AF⊥平面CDE,∴平面BCE⊥平面CDE,证明如下:
△ACD为等边三角形,F为CD中点;
∴AF⊥CD;
∵DE⊥平面ACD,AF?平面ACD;
∴DE⊥AF,即AF⊥DE,DE∩CD=D;
∴AF⊥平面CDE;
由(1)知,BM∥AF;
∴BM⊥平面CDE,BM?平面BCE;
∴平面BCE⊥平面CDE.
点评 考查三角形中位线的性质,平行线的性质:平行线中一条垂直于一个平面,另一条也垂直于这个平面;同时垂直于一个平面的两直线平行,平行四边形的定义,以及线面平行、线面垂直,以及面面垂直的判定定理.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{2}$,0) | B. | (-$\sqrt{2}$,$\sqrt{2}$) | C. | (-$\sqrt{2}$,-1) | D. | (-$\sqrt{2}$,-1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com