
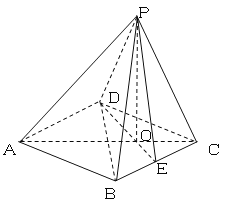
【题目】如图,已知四棱锥P-ABCD的底面是边长为2的菱形,∠BCD=60°,点E是BC边
的中点,AC,DE交于点O,![]() ,且PO⊥平面ABCD.
,且PO⊥平面ABCD.
(1)求证:PD⊥BC;
(2)在线段AP上找一点F,使得BF∥平面PDE,并求此时四面体PDEF的体积.
【答案】(1)证明见解析.
(2) VP-BDE=1.
【解析】
(1)先证明BC⊥平面PDE,即证PD⊥BC.(2)取AP中点为F,再取PD中点为G,连结FG,再证明FG⊥平面PDE,最后求四面体PDEF的体积.
(1)由题可得△BCD为正三角形,E为BC中点,故DE⊥BC.
又PO⊥平面ABCD,BC![]() 平面ABCD,则PO⊥BC,
平面ABCD,则PO⊥BC,
而DE∩PO=O,![]() 平面
平面![]() ,
,
所以BC⊥平面PDE.
又PD![]() 平面PDE,故PD⊥BC.
平面PDE,故PD⊥BC.
(2)取AP中点为F,再取PD中点为G,连结FG.
则FG为△PAD中位线,故FG ![]()
![]() AD,
AD,
又BE ![]()
![]() AD,所以FG
AD,所以FG![]() BE,于是四边形BFGE为平行四边形,
BE,于是四边形BFGE为平行四边形,
因此BF∥EG.又BF![]() 平面PDE,EG
平面PDE,EG![]() 平面PDE,
平面PDE,
所以BF∥平面PDE.
由(1)知,BC⊥平面PDE.则有BC⊥PE,BC⊥DE,
而BC∥FG,故FG⊥PE,FG⊥DE,且DE∩PE=E,
所以FG⊥平面PDE.
于是四面体PDEF的体积为V=![]() S△PDE·FG=
S△PDE·FG=![]() ×
×![]() ×2
×2![]() ×
×![]() ×1=1.
×1=1.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() ,若椭圆上一点与其中心及长轴一个端点构成等腰直角三角形.
,若椭圆上一点与其中心及长轴一个端点构成等腰直角三角形.
(Ⅰ)求椭圆E的离心率;
(Ⅱ)如图,若直线l与椭圆相交于AB且AB是圆![]() 的一条直径,求椭圆E的标准方程.
的一条直径,求椭圆E的标准方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() (
(![]() ).
).
(1)计算![]() ,
,![]() ,
,![]() ,
,![]() ,并求数列
,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求证:数列
,求证:数列![]() 是等比数列;
是等比数列;
(3)由数列![]() 的项组成一个新数列
的项组成一个新数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() 为数列
为数列![]() 的前
的前![]() 项和,试求
项和,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙二人用4张扑克牌(分别是红桃2,红桃3,红桃4,方片4)完游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
(1)设![]() 分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况;
分别表示甲、乙抽到的牌的数字,写出甲乙二人抽到的牌的所有情况;
(2)若甲抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?
(3)甲乙约定:若甲抽到的牌的牌面数字比乙大,则甲胜,反之,则乙胜,你认为此游戏是否公平,说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为建设美丽乡村,政府欲将一块长12百米,宽5百米的矩形空地ABCD建成生态休闲园,园区内有一景观湖EFG(图中阴影部分).以AB所在直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系xOy(如图所示).景观湖的边界曲线符合函数![]() 模型.园区服务中心P在x轴正半轴上,PO=
模型.园区服务中心P在x轴正半轴上,PO=![]() 百米.
百米.

(1)若在点O和景观湖边界曲线上一点M之间修建一条休闲长廊OM,求OM的最短长度;
(2)若在线段DE上设置一园区出口Q,试确定Q的位置,使通道直线段PQ最短.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人玩一种游戏,每次由甲、乙各出1到5根手指,若和为偶数算甲赢,否则算乙赢.
(1)若以![]() 表示和为6的事件,求
表示和为6的事件,求![]() ;
;
(2)现连玩三次,若以![]() 表示甲至少赢一次的事件,
表示甲至少赢一次的事件,![]() 表示乙至少赢两次的事件,试问
表示乙至少赢两次的事件,试问![]() 与
与![]() 是否为互斥事件?为什么?
是否为互斥事件?为什么?
(3)这种游戏规则公平吗?试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有120粒试验种子需要播种,现有两种方案:方案一:将120粒种子分种在40个坑内,每坑3粒;方案二:120粒种子分种在60个坑内,每坑2粒 如果每粒种子发芽的概率为0.5,并且,若一个坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种(每个坑至多补种一次,且第二次补种的种子颗粒同第一次).假定每个坑第一次播种需要2元,补种1个坑需1元;每个成活的坑可收货100粒试验种子,每粒试验种子收益1元.
(1)用![]() 表示播种费用,分别求出两种方案的
表示播种费用,分别求出两种方案的![]() 的数学期望;
的数学期望;
(2)用![]() 表示收益,分别求出两种方案的收益
表示收益,分别求出两种方案的收益![]() 的数学期望;
的数学期望;
(3)如果在某块试验田对该种子进行试验,你认为应该选择哪种方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com