
【题目】设![]() ,
,![]() .
.
(1)令![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)当![]() 时,证明
时,证明![]() .
.
【答案】(1)当![]() 时,函数
时,函数![]() 单调递增区间为
单调递增区间为![]() ;当
;当![]() 时,函数
时,函数![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)求出![]() 的导数,
的导数,![]() ,分
,分![]() 讨论,分别由
讨论,分别由![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间,![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)只要证明
的减区间;(2)只要证明![]() 即可,由(1)知,
即可,由(1)知,![]() ,证明
,证明![]() 在
在![]() 即可.
即可.
试题解析:(1)由![]() ,
,![]() .
.
可得![]() .
.![]()
当![]() 时,
时, ![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
当![]() 时,
时,![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
所以,当![]() 时,函数
时,函数![]() 单调递增区间为
单调递增区间为![]() ;当
;当![]() 时,函数
时,函数![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
(2)只要证明对任意![]() ,
,![]() .
.
由(1)知,![]() 在
在![]() 取得最大值,
取得最大值,
且![]() .
.
令![]() ,
,![]() ,
,
则![]() 在
在![]() 上单调递增,
上单调递增,![]() .
.
所以当![]() 时,
时,![]() 即
即![]() .
.
【方法点晴】本题主要考查的是利用导数研究函数的单调性、利用导数研究函数的最值、利用导数证明不等式,属于难题.利用导数研究函数![]() 的单调性进一步求函数最值的步骤:①确定函数
的单调性进一步求函数最值的步骤:①确定函数![]() 的定义域;②对
的定义域;②对![]() 求导;③令
求导;③令![]() ,解不等式得
,解不等式得![]() 的范围就是递增区间;令
的范围就是递增区间;令![]() ,解不等式得
,解不等式得![]() 的范围就是递减区间;④根据单调性求函数
的范围就是递减区间;④根据单调性求函数![]() 的极值及最值(闭区间上还要注意比较端点处函数值的大小).
的极值及最值(闭区间上还要注意比较端点处函数值的大小).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
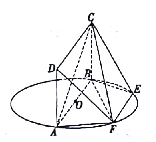
【题目】如图, ![]() 为圆
为圆![]() 的直径,点
的直径,点![]() 在圆
在圆![]() 上,且
上,且![]() ,矩形
,矩形![]() 所在的平面和圆
所在的平面和圆![]() 所在的平面垂直,且
所在的平面垂直,且![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在了点
上是否存在了点![]() ,使得
,使得![]() 平面
平面![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数y=f(x)的图象过点(8,m)和(9,3).
(Ⅰ)求m的值;
(Ⅱ)若函数g(x)=logaf(x)(a>0,a≠1)在区间[16,36]上的最大值比最小值大1,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin2x+2 ![]() sinxsin(x+
sinxsin(x+ ![]() )(ω>0).
)(ω>0).
(1)求f(x)的最小正周期;
(2)求函数f(x)在区间[0, ![]() ]上的取值范围.
]上的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
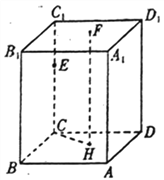
【题目】如图所示,直平行六面体![]() 中,
中,![]() 为棱
为棱![]() 上任意一点,
上任意一点,![]() 为底面
为底面![]() (除
(除![]() 外)上一点,已知
外)上一点,已知![]() 在底面
在底面![]() 上的射影为
上的射影为![]() ,若再增加一个条件,就能得到
,若再增加一个条件,就能得到![]() ,现给出以下条件:
,现给出以下条件:
①![]() ;②
;②![]() 在
在![]() 上;③
上;③![]() 平面
平面![]() ;④直线
;④直线![]() 和
和![]() 在平面
在平面![]() 的射影为同一条直线.其中一定能成为增加条件的是__________.(把你认为正确的都填上)
的射影为同一条直线.其中一定能成为增加条件的是__________.(把你认为正确的都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC是边长为1的正三角形,点P1 , P2 , P3四等分线段BC(如图所示).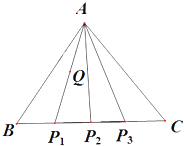
(1)求 ![]()
![]() +
+ ![]()
![]() 的值;
的值;
(2)Q为线段AP1上一点,若 ![]() =m
=m ![]() +
+ ![]()
![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在店庆一周年开展“购物折上折活动”:商场内所有商品按标价的八折出售,折后价格每满500元再减100元.如某商品标价为1500元,则购买该商品的实际付款额为1500×0.8-200=1000(元).设购买某商品得到的实际折扣率![]() .设某商品标价为
.设某商品标价为![]() 元,购买该商品得到的实际折扣率为
元,购买该商品得到的实际折扣率为![]() .
.
(Ⅰ)写出当![]() 时,
时, ![]() 关于
关于![]() 的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
(Ⅱ)对于标价在[2500,3500]的商品,顾客购买标价为多少元的商品,可得到的实际折扣率低于![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A、B、C三种家电,经市场调查决定调整生产方案,计划本季度(按不超过480个工时计算)生产A、B、C三种家电共120台,其中A家电至少生产20台,已知生产A、B、C三种家电每台所需的工时分别为3、4、6个工时,每台的产值分别为20、30、40千元,则按此方案生产,此季度最高产值为( )千元.
A. 3600 B. 350 C. 4800 D. 480
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com