
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面积S=![]() c2,求sin C的值.
c2,求sin C的值.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)求函数f(x)的单调区间;
(2)若g(x)=xf(x)+mx在区间(0,e]上的最大值为﹣3,求m的值;
(3)若x≥1时,有不等式f(x)≥ ![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 为参数),
为参数),![]() 为参数).
为参数).
(1)化![]() 的参数方程为普通方程,并说明它们分别表示什么曲线;
的参数方程为普通方程,并说明它们分别表示什么曲线;
(2)若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() 为
为![]() 上的动点,求
上的动点,求![]() 的中点
的中点![]() 到直线
到直线![]() 为参数)距离的最小值.
为参数)距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(﹣∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”.现有定义在(﹣∞,0)∪(0,+∞)上的如下函数:①f(x)=x2;②f(x)=2x;③f(x)= ![]() ;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
A.①②
B.③④
C.①③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】线段AB外有一点C,∠ABC=60°,AB=200 km,汽车以80 km/h的速度由A向B行驶,同时摩托车以50 km/h的速度由B向C行驶,则运动开始________h后,两车的距离最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(I)已知函数f(x)=rx﹣xr+(1﹣r)(x>0),其中r为有理数,且0<r<1.求f(x)的最小值;
(II)试用(I)的结果证明如下命题:设a1≥0,a2≥0,b1 , b2为正有理数,若b1+b2=1,则a1b1a2b2≤a1b1+a2b2;
(III)请将(II)中的命题推广到一般形式,并用数学归纳法证明你所推广的命题.注:当α为正有理数时,有求导公式(xα)r=αxα﹣1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB、CD是圆的两条平行弦,BE∥AC,BE交CD于E、交圆于F,过A点的切线交DC的延长线于P,PC=ED=1,PA=2.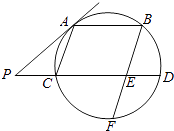
(1)求AC的长;
(2)试比较BE与EF的长度关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的数列{an}的首项a1=1,sn是数列{an}的前n项和,且满足:
anSn+1﹣an+1Sn+an﹣an+1=λanan+1(λ≠0,n∈N )
(1)若a1 , a2 , a3成等比数列,求实数λ的值;
(2)若λ= ![]() ,求Sn .
,求Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com