
【题目】如图1,已知四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,且
,且![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 折到
折到![]() 位置(如图2),使得
位置(如图2),使得![]() 平面
平面![]() ,连结
,连结![]() ,构成一个四棱锥
,构成一个四棱锥![]() .
.

(1)求证![]() ;
;
(2)求二面角![]() 的大小.
的大小.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题(1)可利用分析法寻找思路:由于![]() ,所以要证
,所以要证![]() ,只需证明
,只需证明![]() 平面
平面![]() ,因此只需证
,因此只需证![]() ,这可根据条件
,这可根据条件![]() 平面
平面![]() 得到;(2)求二面角大小,一般方法为利用空间向量数量积求解,即先根据题意建立空间直角坐标系,设立各点坐标,利用方程组解出各面的法向量,利用向量数量积可求法向量的夹角,最后根据法向量夹角与二面角之间关系得结果.
得到;(2)求二面角大小,一般方法为利用空间向量数量积求解,即先根据题意建立空间直角坐标系,设立各点坐标,利用方程组解出各面的法向量,利用向量数量积可求法向量的夹角,最后根据法向量夹角与二面角之间关系得结果.
试题解析:(1)证明:在图1中,∵![]() ,
,![]() ,
,
∴![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
当![]() 沿
沿![]() 折起时,
折起时,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
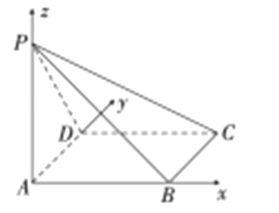
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则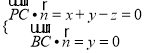 ,取
,取![]() ,得
,得![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]()
则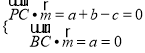 ,取
,取![]() ,得
,得![]() ,
,
设二面角![]() 的大小为
的大小为![]() ,观察图形可知,二面角
,观察图形可知,二面角![]() 为钝角,
为钝角,
则![]() ,∴
,∴![]() ,
,
∴二面角![]() 的大小为
的大小为![]() .
.


科目:高中数学 来源: 题型:
【题目】某高校自主招生一次面试成绩的茎叶图和频率分布直方图均收到了不同程度的损坏,其可见部分信息如下,据此解答下列问题:
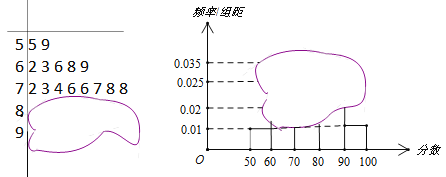
(1)求参加此次高校自主招生面试的总人数![]() 、面试成绩的中位数及分数在
、面试成绩的中位数及分数在![]() 内的人数;
内的人数;
(2)若从面试成绩在![]() 内的学生中任选三人进行随机复查,求恰好有二人分数在
内的学生中任选三人进行随机复查,求恰好有二人分数在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O。D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形。沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥。当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商场销售某种商品的经验表明,该商品每日的销售量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (单位:元/千克)满足关系式
(单位:元/千克)满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
(1) 求![]() 的值;
的值;
(2) 若商品的成品为3元/千克, 试确定销售价格![]() 的值,使商场每日销售该商品所获得的利润最大
的值,使商场每日销售该商品所获得的利润最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数![]() 满足以下三个条件:①对于任意的
满足以下三个条件:①对于任意的![]() ,都有
,都有![]() ;②对于任意的
;②对于任意的![]() 都有
都有![]() ③函数
③函数![]() 的图象关于y轴对称,则下列结论中正确的是( )
的图象关于y轴对称,则下列结论中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() ,
, ![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
, ![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)利用极坐标与直角坐标的互化公式可得直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
,消去参数![]() 可知曲线
可知曲线![]() 是圆心为
是圆心为![]() ,半径为
,半径为![]() 的圆,由直线
的圆,由直线![]() 与曲线
与曲线![]() 相切,可得:
相切,可得: ![]() ;则曲线C的方程为
;则曲线C的方程为![]() , 再次利用极坐标与直角坐标的互化公式可得
, 再次利用极坐标与直角坐标的互化公式可得
可得曲线C的极坐标方程.
(2)由(1)不妨设M(![]() ),
),![]() ,(
,(![]() ),
),
![]() ,
,
![]() ,
,
由此可求![]() 面积的最大值.
面积的最大值.
试题解析:(1)由题意可知直线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
曲线![]() 是圆心为
是圆心为![]() ,半径为
,半径为![]() 的圆,直线
的圆,直线![]() 与曲线
与曲线![]() 相切,可得:
相切,可得:  ;可知曲线C的方程为
;可知曲线C的方程为![]() ,
,
所以曲线C的极坐标方程为![]() ,
,
即![]() .
.
(2)由(1)不妨设M(![]() ),
),![]() ,(
,(![]() ),
),
![]() ,
,

![]() ,
,
当![]() 时,
时, ![]() ,
,
所以△MON面积的最大值为![]() .
.
【题型】解答题
【结束】
23
【题目】已知函数![]() 的定义域为
的定义域为![]() ;
;
(1)求实数![]() 的取值范围;
的取值范围;
(2)设实数![]() 为
为![]() 的最大值,若实数
的最大值,若实数![]() ,
, ![]() ,
, ![]() 满足
满足![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com