直线x+a2y+1=0与直线(a2+1)x-by+3=0互相垂直,a、b∈R且ab≠0,则|ab|的最小值为 .
【答案】
分析:由题意知,两直线的斜率之积等于-1,得到a、b的关系,代入|ab|的解析式变形后使用基本不等式,求得其最小值.
解答:解:由题意得-
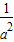
×

=-1,∴a
2 b=a
2+1,b=

=1+
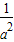
,
∴|ab|=|a×(1+
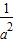
)|=|a+
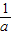
|=|a|+|
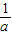
|≥2,当且仅当 a=1 或 a=-1时,取等号.
故|ab|的最小值为2,
故答案为2.
点评:本题考查两条直线垂直的性质,利用基本不等式求式子的最小值,注意检验最小值取得的条件是否具备.
