
若地球半径为R,在北纬45°圈上有A、B两点,且这两点间的球面距离为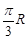 ,则北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的余弦值为 ( )
,则北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的余弦值为 ( )
(A)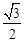 (B)
(B)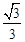 (C)
(C)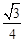 (D)
(D)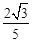
B
【解析】A、B两点间的球面距离为以O为圆心,且过A,B的圆中弧AB的长度,
设∠AOB=α,则α•R=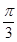 R,α=
R,α=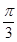 ,又OA=OB,∴△AOB为正三角形,∴AB=R.
,又OA=OB,∴△AOB为正三角形,∴AB=R.
设Q为北纬45°圈的圆心,则由球的截面圆形状可知,OQ⊥⊙Q面,∠OAQ=45°,
且截面圆半径长QA=R•cos∠OAQ=R•cos45°= 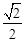 R.在△QAB中,
R.在△QAB中, 得△QAB为等腰直角三角形.设M为AB中点,连接QM,OM,则OM⊥AB,QM⊥AB,
得△QAB为等腰直角三角形.设M为AB中点,连接QM,OM,则OM⊥AB,QM⊥AB,
∴∠OMQ为北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的平面角.
在RT△OMQ中,cos∠OMQ=QM/OM ==  ,所以所求二面角的余弦值是
,所以所求二面角的余弦值是 ,故选B.
,故选B.


科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖北省部分重点中学高三第二次联考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com