
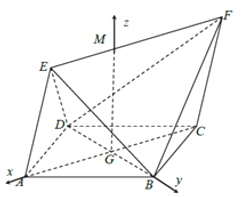
【题目】如图,四边形![]() 为平行四边形,且
为平行四边形,且![]() ,点
,点![]() ,
,![]() 为平面
为平面![]() 外两点,
外两点,![]() 且
且![]() ,
,![]() .
.
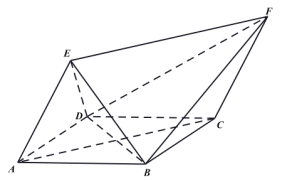
(1)在多面体![]() 中,请写出一个与
中,请写出一个与![]() 垂直的平面,并说明理由;
垂直的平面,并说明理由;
(2)若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
【答案】(1)![]() 平面
平面![]() ,理由见解析;(2)
,理由见解析;(2)![]() .
.
【解析】
(1)设![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,先证
,先证![]() ,再证
,再证![]() ,即可证明
,即可证明![]() 平面
平面![]() ;
;
(2)在平面![]() 内,过
内,过![]() 作
作![]() 的垂线,交
的垂线,交![]() 于
于![]() 点,由(1)可知,平面
点,由(1)可知,平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,故直线
,故直线![]() ,
,![]() ,
,![]() 两两互相垂直,分别以
两两互相垂直,分别以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,利用向量法求出直线
,利用向量法求出直线![]() 与平面
与平面![]() 所成的角即可.
所成的角即可.
(1)![]() 平面
平面![]() ,理由如下:
,理由如下:
设![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,
由题可知,![]() ,
,![]() ,
,![]() ,
,
所以,![]() ,即
,即![]() ,
,
在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以,![]() ,所以
,所以![]() ,故
,故![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ;
;
(2)如图,在平面![]() 内,过
内,过![]() 作
作![]() 的垂线,交
的垂线,交![]() 于
于![]() 点,由(1)可知,平面
点,由(1)可知,平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,故直线
,故直线![]() ,
,![]() ,
,![]() 两两互相垂直,
两两互相垂直,
分别以![]() ,
,![]() ,
,![]() 为
为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,
,
因为![]() ,
,
则![]() ,
,![]() ,
,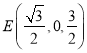 ,
,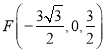 ,
,
所以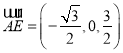 ,
, ,
,
![]() ,
,
设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则
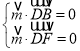 即
即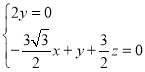 ,解得
,解得 ,
,
取![]() ,则
,则![]() ,
,
所以,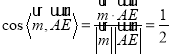 ,
,
故直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.


科目:高中数学 来源: 题型:
【题目】甲、乙二人进行一次象棋比赛,每局胜者得1分,负者得0分(无平局),约定一方得4分时就获得本次比赛的胜利并且比赛结束,设在每局比赛中,甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立,已知前3局中,甲得1分,乙得2分.
,各局比赛结果相互独立,已知前3局中,甲得1分,乙得2分.
(1)求甲获得这次比赛胜利的概率;
(2)设![]() 表示从第4局开始到比赛结束所进行的局数,求
表示从第4局开始到比赛结束所进行的局数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于命题的说法错误的是( )
A.命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”
”
B.“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
C.“若![]() 为
为![]() 的极值点,则
的极值点,则![]() ”的逆命题为真
”的逆命题为真
D.命题![]() :
:![]() ,
,![]() 的否定是
的否定是![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年湖北抗击新冠肺炎期间,全国各地医护人员主动请缨,支援湖北.某地有3名医生,6名护士来到武汉,他们被随机分到3家医院,每家医院1名医生、2名护士,则医生甲和护士乙分到同一家医院的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.

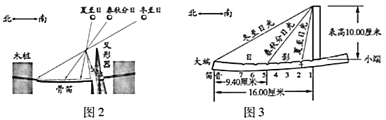
由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表:
黄赤交角 |
|
|
|
|
|
正切值 | 0.439 | 0.444 | 0.450 | 0.455 | 0.461 |
年代 | 公元元年 | 公元前2000年 | 公元前4000年 | 公元前6000年 | 公元前8000年 |
根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( )
A.公元前2000年到公元元年B.公元前4000年到公元前2000年
C.公元前6000年到公元前4000年D.早于公元前6000年
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com