
【题目】下列图象中,可能是函数![]() 的图象的是( )
的图象的是( )
A. 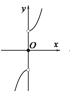 B.
B. 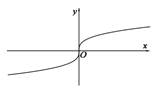
C. 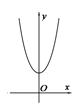 D.
D. 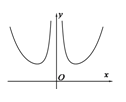
【答案】D
【解析】
根据题意,求出函数的导数,按a的值分5种情况讨论,分析函数f(x)的定义域、是否经过原点以及在第一象限的单调性,综合即可得答案.
根据题意,函数f(x)=xa(ex+e﹣x),其导数f′(x)=axa﹣1(ex+e﹣x)+xa(ex﹣e﹣x),
又由a∈Z,
当a=0,f(x)=ex+e﹣x,(x≠0)其定义域为{x|x≠0},f(x)为偶函数,不经过原点且在第一象限为增函数,没有选项符合;
当a为正偶数时,f(x)=xa(ex+e﹣x),其定义域为R,f(x)为偶函数且过原点,在第一象限为增函数,没有选项符合,
当a为正奇数时,f(x)=xa(ex+e﹣x),其定义域为R,f(x)为奇函数且过原点,在第一象限为增函数且增加的越来越快,没有选项符合,
当a为负偶数时,f(x)=xa(ex+e﹣x),其定义域为{x|x≠0},f(x)为偶函数,不经过原点且在第一象限先减后增,D选项符合;
当a为负奇数时,f(x)=xa(ex+e﹣x),其定义域为{x|x≠0},f(x)为奇函数,不经过原点且在第一象限先减后增,没有选项符合,
综合可得:D可能是函数f(x)=xa(ex+e﹣x)(a∈Z)的图象;
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】互联网使我们的生活日益便捷,网络外卖也开始成为不少人日常生活中不可或缺的一部分,某市一调查机构针对该市市场占有率较高的甲、乙两家网络外卖企业(以下外卖甲、外卖乙)的经营情况进行了调查,调查结果如下表:
1日 | 2日 | 3日 | 4日 | 5日 | |
外卖甲日接单x(百单) | 5 | 2 | 9 | 8 | 11 |
外卖乙日接单y(百单) | 2 | 3 | 10 | 5 | 15 |
(1)试根据表格中这五天的日接单量情况,从统计的角度说明这两家外卖企业的经营状况;
(2)据统计表明,y与x之间具有线性关系.
①请用相关系数r对y与x之间的相关性强弱进行判断;(若![]() ,则可认为y与x有较强的线性相关关系(r值精确到0.001))
,则可认为y与x有较强的线性相关关系(r值精确到0.001))
②经计算求得y与x之间的回归方程为![]() ,假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于25百单时,外卖甲所获取的日纯利润的大致范围.(x值精确到0.01)
,假定每单外卖业务企业平均能获纯利润3元,试预测当外卖乙日接单量不低于25百单时,外卖甲所获取的日纯利润的大致范围.(x值精确到0.01)
相关公式: ,
,
参考数据: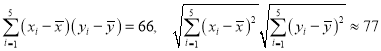 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数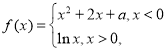 其中
其中![]() 为实数.设
为实数.设![]() ,
,![]() 为该函数图象上的两个不同的点.
为该函数图象上的两个不同的点.
(1)指出函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 的图象在点
的图象在点![]() ,
,![]() 处的切线互相平行,求
处的切线互相平行,求![]() 的最小值;
的最小值;
(3)若函数![]() 的图象在点
的图象在点![]() ,
,![]() 处的切线重合,求
处的切线重合,求![]() 的取值范围.(只要求写出答案).
的取值范围.(只要求写出答案).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,且
轴上运动,且![]() ,若动点
,若动点![]() 满足
满足![]() .
.
(1)求出动点P的轨迹对应曲线C的标准方程;
(2)一条纵截距为2的直线![]() 与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
与曲线C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内一个动点M到定点F(3,0)的距离和它到定直线l:x=6的距离之比是常数![]() .
.
(1)求动点M的轨迹T的方程;
(2)若直线l:x+y-3=0与轨迹T交于A,B两点,且线段AB的垂直平分线与T交于C,D两点,试问A,B,C,D是否在同一个圆上?若是,求出该圆的方程;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,
,![]() 是椭圆上关于原点
是椭圆上关于原点![]() 对称的两个动点,当点
对称的两个动点,当点![]() 的坐标为
的坐标为![]() 时,
时,![]() 的周长恰为
的周长恰为![]() .
.
(1)求椭圆的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,且
两点,且![]()
![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 的棱长均为6,其内有
的棱长均为6,其内有![]() 个小球,球
个小球,球![]() 与三棱锥
与三棱锥![]() 的四个面都相切,球
的四个面都相切,球![]() 与三棱锥
与三棱锥![]() 的三个面和球
的三个面和球![]() 都相切,如此类推,…,球
都相切,如此类推,…,球![]() 与三棱锥
与三棱锥![]() 的三个面和球
的三个面和球![]() 都相切(
都相切(![]() ,且
,且![]() ),则球
),则球![]() 的体积等于__________,球
的体积等于__________,球![]() 的表面积等于__________.
的表面积等于__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com