
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线
处的切线![]() 与
与![]() 有且只有一个公共点,求
有且只有一个公共点,求![]() 的值;
的值;
(2)求证:函数![]() 存在单调递减区间
存在单调递减区间![]() ,并求出单调递减区间的长度
,并求出单调递减区间的长度![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】2018年2月9-25日,第23届冬奥会在韩国平昌举行.4年后,第24届冬奥会将在中国北京和张家口举行.为了宣传冬奥会,某大学在平昌冬奥会开幕后的第二天,从全校学生中随机抽取了120名学生,对是否收看平昌冬奥会开幕式情况进行了问卷调查,统计数据如下:
收看 | 没收看 | |
男生 | 60 | 20 |
女生 | 20 | 20 |
(Ⅰ)根据上表说明,能否有![]() 的把握认为,收看开幕式与性别有关?
的把握认为,收看开幕式与性别有关?
(Ⅱ)现从参与问卷调查且收看了开幕式的学生中,采用按性别分层抽样的方法选取8人,参加2022年北京冬奥会志愿者宣传活动.
(ⅰ)问男、女学生各选取多少人?
(ⅱ)若从这8人中随机选取2人到校广播站开展冬奥会及冰雪项目宣传介绍,求恰好选到一名男生一名女生的概率P.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是城市慢行系统的一种创新模式,对于解决民众出行“最后一公里”的问题特别见效,由于停取方便、租用价格低廉,各色共享单车受到人们的热捧.某自行车厂为共享单车公司生产新样式的单车,已知生产新样式单车的固定成本为20 000元,每生产一辆新样式单车需要增加投入100元.根据初步测算,自行车厂的总收益(单位:元)满足分段函数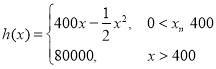 其中x是新样式单车的月产量(单位:辆),利润=总收益-总成本.
其中x是新样式单车的月产量(单位:辆),利润=总收益-总成本.
(1)试将自行车厂的利润y元表示为月产量x的函数;
(2)当月产量为多少件时自行车厂的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,记从“田字型”网格(由四个边长为1的正方形构成)的九个交点中任取三点构成的三角形面积为ξ(当所取的三点共线时,ξ=0),则ξ的数学期望![]() =_________。
=_________。
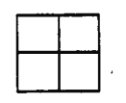
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查全市学生的数学高考成绩,随机地抽取某中学甲、乙两班各10名同学,获得成绩数据如下(单位:分).
甲:132,108,112,121,113,121,118,128,118,129;
乙:133,107,120,113,122,114,128,118,129,127.
(1)画出甲、乙两班学生数学成绩的茎叶图,并根据茎叶图判断哪个班的平均水平较高;
(2)若数学成绩不低于120分,则称为“优秀”,求从这20名学生中随机选取三人,至多有一人是优秀的概率;
(3)以这20人的样本数据来估计整个学校的总体成绩,若从该校(人数很多)任选三人,记![]() 表示抽到优秀学生的人数,求
表示抽到优秀学生的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元。
(1)分别写出两类产品的收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,怎样分配资金才能获得最大收益?其最大收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() ,
,![]() .
.
(1)求直线![]() 与圆
与圆![]() 相切的概率;
相切的概率;
(2)将![]() ,
,![]() ,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
,5的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com