
【题目】设![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)在锐角![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() 若
若![]() ,
, ![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)增区间![]() ,减区间为
,减区间为![]() ;(2)
;(2)![]()
【解析】试题分析:(1)将函数化为![]() ,然后根据正弦函数的单调区间求解;
,然后根据正弦函数的单调区间求解;
(2)由![]() 求得
求得![]() ,然后根据余弦定理得到
,然后根据余弦定理得到![]() ,由基本不等式可得
,由基本不等式可得![]() ,进而可得三角形面积的最大值。
,进而可得三角形面积的最大值。
试题解析:
(1)由题意知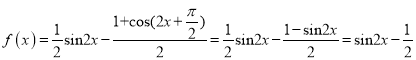 ,
,
由-![]() +2kπ≤2x≤
+2kπ≤2x≤![]() +2kπ,k∈Z,
+2kπ,k∈Z,
可得-![]() +kπ≤x≤
+kπ≤x≤![]() +kπ,k∈Z;
+kπ,k∈Z;
由![]() +2kπ≤2x≤
+2kπ≤2x≤![]() +2kπ,k∈Z,
+2kπ,k∈Z,
可得![]() +kπ≤x≤
+kπ≤x≤![]() +kπ,k∈Z.
+kπ,k∈Z.
所以f(x)的单调递增区间是[-![]() +kπ,
+kπ, ![]() +kπ](k∈Z);单调递减区间是[
+kπ](k∈Z);单调递减区间是[![]() +kπ,
+kπ, ![]() +kπ](k∈Z).
+kπ](k∈Z).
(2)由f(![]() )=sinA-
)=sinA-![]() =0,得sinA=
=0,得sinA=![]() ,
,
由题意知A为锐角,
所以cosA=![]() ,
,
由余弦定理得![]() ,
,
所以![]() ,当且仅当b=c时等号成立,
,当且仅当b=c时等号成立,
所以![]() ,
,
所以![]()
所以△ABC面积的最大值为![]() 。
。


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+ax2+bx+c在x=﹣ ![]() 与x=1时都取得极值.
与x=1时都取得极值.
(1)求a、b的值与函数f(x)的单调区间;
(2)若对x∈[﹣1,2],不等式f(x)<c2恒成立,求c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣ax2+(2﹣a)x. (Ⅰ)讨论f(x)的单调性;
(Ⅱ)设a>0,证明:当0<x< ![]() 时,f(
时,f( ![]() +x)>f(
+x)>f( ![]() ﹣x);
﹣x);
(Ⅲ)若函数y=f(x)的图象与x轴交于A,B两点,线段AB中点的横坐标为x0 , 证明:f′(x0)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某城市有一块半径为40m的半圆形(以O为圆心,AB为直径)绿化区域,现计划对其进行改建.在AB的延长线上取点D,使OD=80m,在半圆上选定一点C,改建后的绿化区域由扇形区域AOC和三角形区域COD组成,其面积为S m2. 设∠AOC=x rad.
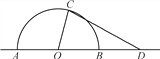
(1)写出S关于x的函数关系式S(x),并指出x的取值范围;
(2)张强同学说:当∠AOC=![]() 时,改建后的绿化区域面积S最大.张强同学的说法正确吗?若不正确,请求出改建后的绿化区域面积S最大值.
时,改建后的绿化区域面积S最大.张强同学的说法正确吗?若不正确,请求出改建后的绿化区域面积S最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin (2x+ ![]() ).
).
(1)求函数f(x)的最小正周期及其单调减区间;
(2)用“五点法”画出函数g(x)=f(x),x∈[﹣ ![]() ,
, ![]() ]的图象(完成列表格并作图),由图象研究并写出g(x)的对称轴和对称中心.
]的图象(完成列表格并作图),由图象研究并写出g(x)的对称轴和对称中心.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com