
����Ŀ��ij�о���ѧϰС��Դ�����ҹ�²��С��ij�������ӷ�ѿ����֮��Ĺ�ϵ�����о������Ƿֱ��¼��3��1����3��5�յ�ÿ����ҹ�²���ʵ����ÿ��ÿ100�����ӽ��ݺ�ķ�ѿ�����õ��������ϣ�
���� | 3��1�� | 3��2�� | 3��3�� | 3��4�� | 3��5�� |
�²�x(��) | 10 | 11 | 13 | 12 | 8 |
��ѿ��y(��) | 23 | 25 | 30 | 26 | 16 |
(1)�����3��2����3��4�յ����ݣ����y����x�����Իع鷽��![]() ��
��
(2)�������Իع鷽�̵õ��Ĺ�����������ѡ���ļ������ݵ�����������2�ţ�����Ϊ�õ������Իع鷽���ǿɿ��ģ�����(1)�����õ����Իع鷽���Ƿ�ɿ���
���𰸡���1��![]() ����2���ɿ�
����2���ɿ�
��������
�����⣨1���ȴ���ʽ��![]() ������ƽ���������
������ƽ���������![]() ��2���������ݵõ�����ֵ������ʵ��ֵ�Ƚϣ�ȷ������1������½���
��2���������ݵõ�����ֵ������ʵ��ֵ�Ƚϣ�ȷ������1������½���
�����������(1)��![]() ��12��
��12��![]() ��27��
��27��
![]() iyi��977��
iyi��977��![]() ��434��
��434��
��![]() ��
��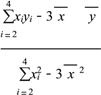 ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��27��
��27��![]() ��12����3��
��12����3��
����������Իع鷽��Ϊy��![]() x��3��
x��3��
(2)��x��10ʱ��y��![]() ��10��3��22��
��10��3��22��
��x��8ʱ��y��![]() ��8��3��17��
��8��3��17��
��������ݵ�����1���������⣬����Ϊ(1)�����õ����Իع鷽���ǿɿ��ģ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣���֪����A={x|-2<x��0}��B={x|y=![]() }
}
��1����RA����B��
��2��������C={x|a��x��2a+1}��CA����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬѧ�μ�һ�����������Ϸ�������κ�һ��ÿ���һ�λ���Ŀ���2�֣�δ����Ŀ���0�֣����ס�����������������ʷֱ�Ϊ ![]() ��P���Ҽס������˸����һ�ε÷�֮��Ϊ2�ĸ���Ϊ
��P���Ҽס������˸����һ�ε÷�֮��Ϊ2�ĸ���Ϊ ![]() ������ס��������������Ӱ�죬��PֵΪ�� ��
������ס��������������Ӱ�죬��PֵΪ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��50��ѧ����һ�ΰ��ײ����У��ɼ�ȫ������13 s��19 s֮�䣬�����Խ���ֳ��������飺[13,14)��[14,15)��[15,16)��[16,17)��[17,18)��[18,19]����ͼ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ����ɼ�С��17 s��ѧ������ռȫ�������İٷֱ�Ϊx���ɼ���[15,17)�е�ѧ������Ϊy�����Ƶ�ʷֲ�ֱ��ͼ�п��Է�����x��y�ֱ�Ϊ (�� ��)
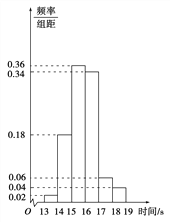
A. 90%,35B. 90%,45
C. 10%,35D. 10%,45
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ABC���ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c��������sinA+sinB=[cosA��cos���Щ�B��]sinC��
��1�����жϡ�ABC����״����˵�����ɣ�
��2����a+b+c=1+ ![]() �������ABC��������ֵ��
�������ABC��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֲ�Ʒ�Ĺ�����֧��![]() ����Ԫ��������
����Ԫ��������![]() ����Ԫ��֮�������µĶ�Ӧ���ݣ�
����Ԫ��֮�������µĶ�Ӧ���ݣ�
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
�������Ͽ�֪![]() ��
��![]() ��������ع�ϵ������
��������ع�ϵ������
��1��������ϱ��ṩ�����ݣ�����С���˷����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
��2���ݴ˹��ƹ�����֧��Ϊ10��Ԫʱ��������![]() ��ֵ.
��ֵ.
���ο���ʽ��
 ��
��![]() .��
.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽����ijУ������ҵ������������Աѧ������������������õ���������������Ƶ�ʷֲ�ֱ��ͼ����ͼ������֪ͼ�д����ҵ�ǰ3��С���Ƶ��֮��Ϊ1��2��3�����е�2С���Ƶ��Ϊ12��
�������У��������Ա����������
����������ѧУ����������������ȫʡ���������ݣ�����ȫʡ��������Ա��ͬѧ�У������ࣩܶ��ѡ���ˣ���X��ʾ���س���60�����ѧ����������X�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У��ڽ�A��B��C���Եı�Ϊa��b��c���� ![]() asinC��c��2+cosA��=0��
asinC��c��2+cosA��=0��
��1�����A�Ĵ�С��
��2������ABC�����߳�Ϊ ![]() ����sinC=2sinB������С�߳���
����sinC=2sinB������С�߳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У��ڽ�A��B��C���Եı߷ֱ�Ϊa��b��c��������sin2B+sin2C=sin2A+2sinBsinCsin��B+C���� �������A�Ĵ�С��
������a=2�����ABC��������ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com