
【题目】已知椭圆E: ![]() 的左、右焦点分别为F1、F2 , 离心率
的左、右焦点分别为F1、F2 , 离心率 ![]() ,P为椭圆E上的任意一点(不含长轴端点),且△PF1F2面积的最大值为1.
,P为椭圆E上的任意一点(不含长轴端点),且△PF1F2面积的最大值为1.
(Ⅰ)求椭圆E的方程;
(Ⅱ)已知直x﹣y+m=0与椭圆E交于不同的两点A,B,且线AB的中点不在圆 ![]() 内,求m的取值范围.
内,求m的取值范围.
【答案】解:(Ⅰ)由 ![]() ,得
,得 ![]() ,
,
又a2=b2+c2,且 ![]() ,
,
联立解得: ![]() ,c=1.
,c=1.
∴椭圆的标准方程为 ![]() ;
;
(Ⅱ)联立 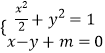 ,消去y整理得:3x2+4mx+2m2﹣2=0.
,消去y整理得:3x2+4mx+2m2﹣2=0.
则△=16m2﹣12(2m2﹣2)=8(﹣m2+3)>0,解得 ![]() .
.
设A(x1,y1),B(x2,y2),则 ![]() ,
,
![]() ,即AB的中点为(
,即AB的中点为( ![]() ).
).
又AB的中点不在圆 ![]() 内,
内,
∴ ![]() ,解得:m≤﹣1或m≥1.
,解得:m≤﹣1或m≥1.
综上可知, ![]() 或1
或1 ![]()
【解析】(Ⅰ)由已知列出关于a、b、c的方程,联立方程求得a、b的值进而求出椭圆的方程。(Ⅱ)联立直线与椭圆的方程,利用一元二次方程的根与系数的关系求得AB中点的坐标,再由AB的中点不在圆内结合判别式可求得m的取值范围。


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】阅读下面材料:
根据两角和与差的正弦公式,有
![]() ------①
------①
![]() ------②
------②
由①+② 得![]() ------③
------③
令![]() 有
有![]()
代入③得![]() .
.
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明:
![]() ;
;
(Ⅱ)若![]() 的三个内角
的三个内角![]() 满足
满足![]() ,试判断
,试判断![]() 的形状.
的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sin(ωx﹣ ![]() )+sin(ωx﹣
)+sin(ωx﹣ ![]() ),其中0<ω<3,已知f(
),其中0<ω<3,已知f( ![]() )=0.
)=0.
(Ⅰ)求ω;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移 ![]() 个单位,得到函数y=g(x)的图象,求g(x)在[﹣
个单位,得到函数y=g(x)的图象,求g(x)在[﹣ ![]() ,
, ![]() ]上的最小值.
]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=log2( ![]() +a).
+a).
(1)当a=5时,解不等式f(x)>0;
(2)若关于x的方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一个元素,求a的取值范围.
(3)设a>0,若对任意t∈[ ![]() ,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过1,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知直线l1:4x﹣3y+6=0和直线l2:x=﹣1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知三点A(-1,0)、B(t,2)、C(2,1),t∈R,O为坐标原点
(I)若△ABC是∠B为直角的直角三角形,求t的值
(Ⅱ)若四边形ABCD是平行四边形,求![]() 的最小值
的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y=ax2(a>0)的焦点到准线的距离为 ![]() ,且C上的两点A(x1 , y1),B(x2 , y2)关于直线y=x+m对称,并且
,且C上的两点A(x1 , y1),B(x2 , y2)关于直线y=x+m对称,并且 ![]() ,那么m= .
,那么m= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次趣味校园运动会的颁奖仪式上,高一、高二、高三代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就座,其中高二代表队有6人.

(1)求n的值;
(2)把在前排就座的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖.求a和b至少有一人上台抽奖的概率;
(3)抽奖活动的规则是:代表通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该代表中奖;若电脑显示“谢谢”,则不中奖,求该代表中奖的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲、乙两种产品所得利润分别为![]() 和
和![]() (万元),它们与投入资金
(万元),它们与投入资金![]() (万元)的关系有经验公式
(万元)的关系有经验公式![]() ,
,![]() ,今将150万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投资金额不低于25万元.
,今将150万元资金投入生产甲、乙两种产品,并要求对甲、乙两种产品的投资金额不低于25万元.
(1)设对乙产品投入资金![]() 万元,求总利润
万元,求总利润![]() (万元)关于
(万元)关于![]() 的函数关系式及其定义域;
的函数关系式及其定义域;
(2)如何分配使用资金,才能使所得总利润最大?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com