
【题目】如图1所示,在直角梯形DCEF中,![]() ,
,![]() ,
,![]() ,
,![]() ,将四边形ABEF沿AB边折成图2.
,将四边形ABEF沿AB边折成图2.
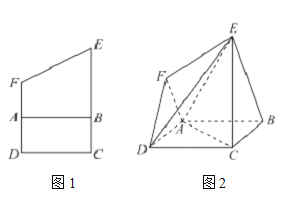
(1)求证:![]() 平面DEF;
平面DEF;
(2)若![]() ,求平面DEF与平面EAC所成锐二面角的余弦值.
,求平面DEF与平面EAC所成锐二面角的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)连接BD,交AC于点O,取DE的中点为G,连接FG,OG,证明![]() ,再利用线面平行判定定理,即可证得
,再利用线面平行判定定理,即可证得![]() 平面DEF;
平面DEF;
(2)以C为坐标原点,CB,CD,CE所在直线分别为x,y,z轴正方向建立空间直角坐标系,求出平面DEF的法向量![]() ,平面EAC的法向量
,平面EAC的法向量![]() ,求出两个法向量夹角的余弦值,从而求得平面DEF与平面EAC所成锐二面角的余弦值。
,求出两个法向量夹角的余弦值,从而求得平面DEF与平面EAC所成锐二面角的余弦值。
(1)连接BD,交AC于点O,取DE的中点为G,连接FG,OG,
则![]() ,
,![]() ,
,
又因为![]() ,
,![]() ,
,
所以![]() ,且
,且![]() ,
,
所以四边形AOGF是平行四边形,
所以![]() ,
,
又![]() 平面DEF,
平面DEF,![]() 平面DEF,
平面DEF,
所以![]() 平面DEF.
平面DEF.
(2)因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
因为![]() ,
,
所以![]() 平面ABCD,
平面ABCD,
所以CB,CD,CE两两垂直,
以C为坐标原点,CB,CD,CE所在直线分别为x,y,z轴正方向建立空间直角坐标系,
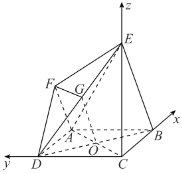
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,
设平面DEF的法向量为![]() ,
,
因为![]() ,
,![]() ,
,
所以由![]() ,
,![]() ,得
,得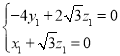 ,
,
令![]() ,得
,得![]() ,
,![]() ,
,
所以![]() ,
,
设平面EAC的法向量![]() ,
,
因为![]() ,
,![]() ,
,
所以由![]() ,
,![]() ,得
,得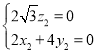 ,
,
令![]() ,得
,得![]() ,
,
设平面DEF与平面EAC所成的锐二面角为![]() ,
,
所以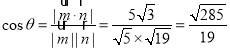 ,
,
所以平面DEF与平面EAC所成的锐二面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】对于在某个区间![]() 上有意义的函数
上有意义的函数![]() ,如果存在一次函数
,如果存在一次函数![]() 使得对于任意的
使得对于任意的![]() ,有
,有![]() 恒成立,则称函数
恒成立,则称函数![]() 是函数
是函数![]() 的一个弱渐近函数.
的一个弱渐近函数.
(1)若函数![]() 是函数
是函数![]() 在区间
在区间![]() 上的一个弱渐近函数,求实数
上的一个弱渐近函数,求实数![]() 的取值范围;
的取值范围;
(2)证明:函数![]() 是函数
是函数![]() 在区间
在区间![]() 上的弱渐近函数;
上的弱渐近函数;
(3)试问:函数![]() 与函数
与函数![]() (其中
(其中![]() 为自然对数的底数)在区间
为自然对数的底数)在区间![]() 上是否存在相同的弱渐近函数?如果存在,请求出对应的弱渐近函数应满足的条件;如不存在,请说明理由.
上是否存在相同的弱渐近函数?如果存在,请求出对应的弱渐近函数应满足的条件;如不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若存在实数
,若存在实数![]() ,使得对于定义域内的任意实数
,使得对于定义域内的任意实数![]() ,均有
,均有![]() 成立,则称函数
成立,则称函数![]() 为“可平衡”函数,有序数对
为“可平衡”函数,有序数对![]() 称为函数
称为函数![]() 的“平衡”数对.
的“平衡”数对.
(1)若![]() ,判断
,判断![]() 是否为“可平衡”函数,并说明理由;
是否为“可平衡”函数,并说明理由;
(2)若![]() ,
,![]() ,当
,当![]() 变化时,求证:
变化时,求证:![]() 与
与![]() 的“平衡”数对相同;
的“平衡”数对相同;
(3)若![]() ,且
,且![]() 、
、![]() 均为函数
均为函数![]() 的“平衡”数对.当
的“平衡”数对.当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第十一届全国少数民族传统体育运动会在河南郑州举行,某项目比赛期间需要安排3名志愿者完成5项工作,每人至少完成一项,每项工作由一人完成,则不同的安排方式共有多少种
A.60B.90C.120D.150
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数),将曲线
为参数),将曲线![]() 上所有点横坐标缩短为原来的
上所有点横坐标缩短为原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]() ,过点
,过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的参数方程和
的参数方程和![]() 的取值范围;
的取值范围;
(2)求![]() 中点
中点![]() 的轨迹的参数方程.
的轨迹的参数方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() ,将函数
,将函数![]() 的图像向右平移
的图像向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图像.
的图像.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)在锐角![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,若
,若![]() ,
,![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.

(1)求在未来的连续4天中,有2天的日销售量低于100枝且另外2天不低于150枝的概率;
(2)用![]() 表示在未来4天里日销售量不低于100枝的天数,求随机变量
表示在未来4天里日销售量不低于100枝的天数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com