练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．解不等式|2x-1|+|x+1|＜3的解集为（-1，1）．

    分析 把要解的不等式等价转化为与之等价的三个不等式组，求出每个不等式组的解集，再取并集，即得所求．

    解答 解：不等式|2x-1|+|x+1|＜3，等价于$\left\{\begin{array}{l}{x＜-1}\\{1-2x-x-1＜3}\end{array}\right.$①，或$\left\{\begin{array}{l}{-1≤x≤\frac{1}{2}}\\{1-2x+x+1＜3}\end{array}\right.$②，或 $\left\{\begin{array}{l}{x＞\frac{1}{2}}\\{2x-1+x+1＜3}\end{array}\right.$．
    解①求得 x∈∅，解②求得-1＜x≤$\frac{1}{2}$，解③求得$\frac{1}{2}$＜x＜1，
    综上可得，不等式的解集为{x|-1＜x＜1}，
    故答案为：（-1，1）．

    点评 本题主要考查绝对值三角不等式，绝对值不等式的解法，体现了转化、分类讨论的数学思想，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=kx+b的图象与x，y轴分别相交于点A、B，$\overrightarrow{AB}$=（2，2），函数g（x）=x2-x-6．
    （1）求k，b的值；
    （2）当x满足f（x）＞g（x）时，求函数$\frac{g（x）+1}{f（x）}$的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知i是虚数单位．若复数z满足（1-i）•z=2i3，则复数z=（　　）
    A．1+iB．1-iC．-1+iD．-1-i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．函数$y=tan（x+\frac{π}{4}）$的单调增区间为（　　）
    A．$[{kπ-\frac{3π}{4}；kπ+\frac{π}{4}}]$B．$（kπ-\frac{3π}{4}，kπ+\frac{π}{4}）$C．$[{kπ-\frac{π}{2}，kπ+\frac{π}{2}}]$D．$（kπ-\frac{π}{2}，kπ+\frac{π}{2}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知向量$\overrightarrow a=（m+1，-3），\overrightarrow b=（1，m-3），（\overrightarrow a+\overrightarrow b）⊥（\overrightarrow a-\overrightarrow b）$，求实数m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．i是虚数单位，若集合S={-1，0，1}，则（　　）
    A．i3∈SB．i6∈SC．（-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i）3⊆SD．{（-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i）2}⊆S

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数f（x）=xlnx．
    （1）求f（x）在（e，f（e））处切线方程；
    （2）求f（x）最小值；
    （3）设F（x）=ax2+f′（x）（a≠0），讨论函数F（x）的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．某班2名同学准备报名参加浙江大学、复旦大学和上海交大的自主招生考试，要求每人最多选报两所学校，且至少报一所学校，则不同的报名结果有36种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

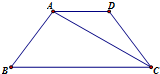    11．如图，等腰梯形ABCD中，AB=AD=DC=$\frac{1}{2}$BC=1，现将三角形ACD沿AC向上折起，满足平面ABC⊥平面ACD，则三棱锥D-ABC的外接球的表面积为5π．

    查看答案和解析>>

    同步练习册答案