
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调减区间;
的单调减区间;
(2)若关于x的不等式![]() 恒成立,求实数a的范围.
恒成立,求实数a的范围.
【答案】(1)![]() (2)a≥﹣2
(2)a≥﹣2
【解析】
(1)求出函数的导数,解关于导函数的不等式,求出函的递减区间即可;
(2)问题等价于![]() 在x∈(0,+∞)上恒成立,令
在x∈(0,+∞)上恒成立,令![]() ,根据函数的单调性求出a的范围即可.
,根据函数的单调性求出a的范围即可.
解(1)f'(x)=3x2+2ax﹣a2=(3x﹣a)(x+a)
由f'(x)<0且a<0得:![]()
∴函数f(x)的单调减区间为![]()
(2)依题意x∈(0,+∞)时,不等式2xlnx≤f'(x)+a2+1恒成立,
等价于![]() 在x∈(0,+∞)上恒成立.
在x∈(0,+∞)上恒成立.
令![]()
则![]()
当x∈(0,1)时,h'(x)>0,h(x)单调递增
当x∈(1,+∞)时,h'(x)<0,h(x)单调递减
∴当x=1时,h(x)取得最大值h(1)=﹣2
故a≥﹣2


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为![]() ,再由乙猜甲刚才想的数字把乙猜的数字记为
,再由乙猜甲刚才想的数字把乙猜的数字记为![]() ,且
,且![]() ,若
,若![]() ,则称甲乙“心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________
,则称甲乙“心有灵犀”,现任意找两个人玩这个游戏,得出他们“心有灵犀”的概率为________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,AB=PA=1,AD![]() ,F是PB中点,E为BC上一点.
,F是PB中点,E为BC上一点.
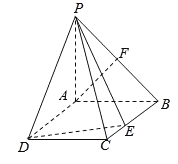
(1)求证:AF⊥平面PBC;
(2)当BE为何值时,二面角C﹣PE﹣D为45°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,等腰梯形MNCD中,MD∥NC,MN=![]() MD=2,∠CDM=60°,E为线段MD上一点,且ME=3,以EC为折痕将四边形MNCE折起,使MN到达AB的位置,且AE⊥DC
MD=2,∠CDM=60°,E为线段MD上一点,且ME=3,以EC为折痕将四边形MNCE折起,使MN到达AB的位置,且AE⊥DC

(1)求证:DE⊥平面ABCE;
(2)求点A到平面DBE的距离
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知定点A(1,0),点M在
中,已知定点A(1,0),点M在![]() 轴上运动,点N在
轴上运动,点N在![]() 轴上运动,点P为坐标平面内的动点,且满足
轴上运动,点P为坐标平面内的动点,且满足![]() .
.
(1)求动点P的轨迹C的方程;
(2)点Q为圆![]() 上一点,由Q向C引切线,切点分别为S、T,记
上一点,由Q向C引切线,切点分别为S、T,记![]() 分别为切线QS,QT的斜率,当Q运动时,求
分别为切线QS,QT的斜率,当Q运动时,求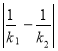 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2018·湖南师大附中摸底)已知直线l经过点P(-4,-3),且被圆(x+1)2+(y+2)2=25截得的弦长为8,则直线l的方程是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com