
【题目】根据某镇家庭抽样调查的统计,2003年每户家庭平均消费支出总额为1万元,其中食品消费额为0.6万元.预测2003年后,每户家庭平均消费支出总额每年增加3000元,如果到2005年该镇居民生活状况能达到小康水平(即恩格尔系数n满足![]() ),则这个镇每户食品消费额平均每年的增长率至多是多少(精确到0.1%)?
),则这个镇每户食品消费额平均每年的增长率至多是多少(精确到0.1%)?
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】如图点![]() 是半径为
是半径为![]() 的砂轮边缘上的一个质点,它从初始位置
的砂轮边缘上的一个质点,它从初始位置![]() (
(![]() ,
,![]() )开始,按逆时针方向每
)开始,按逆时针方向每![]() 旋转一周,
旋转一周,![]() .
.
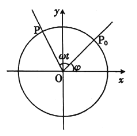
(1)求点![]() 的纵坐标
的纵坐标![]() 关于时间
关于时间![]() 的函数关系;
的函数关系;
(2)求点![]() 的运动周期和频率;
的运动周期和频率;
(3)函数![]() 的图像可由余弦曲线经过怎样的变化得到?
的图像可由余弦曲线经过怎样的变化得到?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为
的圆心为![]() ,直线
,直线![]() 过点
过点![]() 且与
且与![]() 轴不重合,直线
轴不重合,直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.
(1)证明![]() 为定值,并写出点
为定值,并写出点![]() 的轨迹方程;
的轨迹方程;
(2)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,过点
两点,过点![]() 且与直线
且与直线![]() 垂直的直线与圆
垂直的直线与圆![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】乒乓球赛规定:一局比赛,双方比分在10平前,一方连续发球2次后,对方再连续发球2次,依次轮换,每次发球,胜方得1分,负方得0分。设在甲、乙的比赛中,每次发球,甲发球得1分的概率为![]() ,乙发球得1分的概率为
,乙发球得1分的概率为![]() ,各次发球的胜负结果相互独立,甲、乙的一局比赛中,甲先发球.则开始第4次发球时,甲、乙的比分为1比2的概率为________.
,各次发球的胜负结果相互独立,甲、乙的一局比赛中,甲先发球.则开始第4次发球时,甲、乙的比分为1比2的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的导函数为
的导函数为![]() ,且对任意的实数
,且对任意的实数![]() 都有
都有![]() (
(![]() 是自然对数的底数),且
是自然对数的底数),且![]() ,若关于
,若关于![]() 的不等式
的不等式![]() 的解集中恰有两个整数,则实数
的解集中恰有两个整数,则实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分) 已知P(3,2),一直线![]() 过点P,
过点P,
①若直线![]() 在两坐标轴上截距之和为12,求直线
在两坐标轴上截距之和为12,求直线![]() 的方程;
的方程;
②若直线![]() 与x、y轴正半轴交于A、B两点,当
与x、y轴正半轴交于A、B两点,当![]() 面积为12时求直线
面积为12时求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com